Vol. 6, n. 2 ottobre 2020
Pedagogia sociale
Lettura e interpretazione delle problematiche di apprendimento a partire dalle prove di valutazione nazionale
Ricerca pedagogica fra strategie e competenze numeriche
Viviana Malvasi1, Enrico Bocciolesi2 e Antonio Medina Rivilla3
Sommario
La ricerca proposta è stata realizzata con il principale obiettivo di favorire il rendimento degli alunni in matematica nel primo biennio della scuola secondaria di secondo grado, nel contesto del Sud Italia. A seguito delle attività di ricerca sono state elaborate e applicate delle strategie di insegnamento adeguate ai risultati ottenuti e in forza delle competenze da raggiungere, tenendo inoltre presente la formazione necessaria per il corpo docente. Si è partiti dall’analizzare i risultati INVALSI per capire dove si poteva intervenire per poi elaborare un metodo, di seguito chiamato Metodo 360, che potesse aiutare gli studenti nel migliorare i risultati di apprendimento e delle prove INVALSI. Come metodologia di ricerca si è scelto di svolgere un’indagine principalmente quantitativa: uno studio sperimentale di campo dove è stata fissata come variabile indipendente il Metodo 360 e come variabile dipendente il rendimento degli alunni nelle prove INVALSI. Per misurare la variabile dipendente ci si è serviti di un pre-test e un post-test, e tra gli strumenti utilizzati c’è anche una scala di valutazione di tipo Likert di produzione propria e verificata mediante l’Alfa di Cronbach (Nunnally, 1978). Nell’analisi dei risultati si è tenuto conto della media raggiunta nelle varie Dimensioni e nei vari Ambiti, ma anche della deviazione standard.
Parole chiave
Pedagogia, problematiche, complessità, apprendimento.
Social pedagogy
Analysing pedagogical issues through national assessment tests
A pedagogical study on strategies and numerical skills
Viviana Malvasi4, Enrico Bocciolesi5 and Antonio Medina Rivilla6
Abstract
The proposed research was carried out with the main aim of improving pupils’ performance in mathematics in the first two years of secondary school, in the context of Southern Italy. Following the research activities, teaching strategies were developed and applied in line with results obtained and in accordance with skills to be achieved, while also considering the training required for the teaching staff. It started with analysis of the INVALSI results in order to understand where it was necessary to intervene, and then a method, called Method 360, was developed that could help students improve their results in the INVALSI tests. The research methodology selected was a mainly quantitative survey: an experimental field study where Method 360 was set as an independent variable and the performance of pupils in the INVALSI tests as a dependent variable. A pre-test and post-test were used to measure the dependent variable, and among the tools used there was also a Likert-type evaluation scale, which we produced and verified using the Cronbach Alpha (Nunnally, 1978). In analysing the results, the average achieved in the various dimensions and areas was considered, but also the standard deviation.
Keywords
Pedagogy, issues, complexity, learning.
Introduzione
I recenti risultati INVALSI hanno evidenziato delle distanze geografiche attraverso i punteggi ottenuti dagli studenti. Dal 2018 sono stati introdotti anche i livelli, dove per «livello 3» si indica l’obiettivo minimo e sufficiente per sapere matematico. Sicuramente sono innumerevoli le difficoltà legate all’insegnamento di questa disciplina, tra le più incisive c’è probabilmente la scarsa motivazione degli studenti, proveniente da un limitato interesse verso nozioni e contenuti, apparentemente, lontani dal loro quotidiano, o dalle loro credenze sulla disciplina o, peggio ancora, dalle loro esperienze negative pregresse. Quanto appena detto è ciò che troviamo tra le pagine del libro degli autori Di Martino e Zan (2010) dove viene evidenziata la problematica dell’atteggiamento negativo nei confronti della matematica. Un atteggiamento che, secondo gli autori, ha tre dimensioni distinte: 1. la dimensione emozionale; 2. il senso di auto-efficacia; 3.la visione della disciplina.
Tutto ciò induce a uno scarso rendimento in questa disciplina in Italia, e non solo, soprattutto in alcune zone del nostro Paese e in alcuni gradi di scuola. A dare informazioni circa il rendimento in matematica e italiano, a livello nazionale abbiamo l’Istituto Nazionale per la Valutazione del Sistema Educativo di Istruzione e di Formazione (INVALSI), che nell’anno 2020, per causa Covid-19, non ha potuto rilevare nuovi dati. Nel prendere atto della differenza dei risultati ci si è posti la domanda: quanto è eterogeneo il sistema scolastico italiano? L’offerta formativa è omogenea da regione a regione? È della scuola, ci dice Baldacci (2016), il compito di garantire a tutti gli scolari il raggiungimento delle conoscenze e delle competenze fondamentali. Egli parla dell’idea di uguaglianza delle opportunità, sostenendo che il sistema deve garantire a tutti le stesse opportunità, così i risultati dipenderanno solo dal merito personale. Il nostro sistema scolastico nazionale offre a tutti gli studenti le stesse possibilità?
Da ogni Rapporto INVALSI degli ultimi anni emergono rilevanti differenze negli apprendimenti della matematica tra le diverse zone del Paese, e l’area che presenta i risultati più allarmanti risulta essere il Sud e le Isole (Sicilia e Sardegna). Come si evince dal Rapporto Risultati dell’INVALSI 2019, addirittura le differenze aumentano mano a mano che lo studente procede nel suo percorso formativo, cioè al termine del biennio della secondaria di secondo grado le differenze tra Nord e Sud si consolidano e si accentuano rispetto al grado precedente (INVALSI, 2019).
Questa ricerca nasce da una domanda specifica: i docenti di matematica possono fare qualcosa per intervenire e ridurre queste distanze? Ormai si parla molto di contrasto delle disuguaglianze, e i risultati INVALSI ci stanno dicendo che in Italia, purtroppo, esistono in termini di apprendimento, e sono pure ben marcate. Ci ricorda Alessandrini (2017) che l’obiettivo di una società giusta dovrebbe essere la realizzazione dell’eguaglianza delle capacità dei suoi membri; e continua sostenendo che l’obiettivo da massimizzare non è l’utilità: non si tratta solo di redistribuire beni, bensì di attivare le capacità di utilizzare quei beni. Chiariamo fin da subito che siamo consapevoli delle differenze di contesto e dei risultati a disposizione, e probabilmente la differenza degli esiti della prova INVALSI tra Nord e Sud ne è prova. Ad ogni modo siamo pedagogisti, docenti, educatori ed è nostro compito adeguare la strategia al contesto: «la pedagogia può e deve confrontarsi con il tema del contrasto alle disuguaglianze e alla fragilità del capitale umano» (Alessandrini, 2017, p. 26). È nostro dovere cambiare rotta se vediamo che ciò che stiamo facendo non produce i risultati sperati. Con questo primario obiettivo si è iniziato ad analizzare i risultati INVALSI per capire dove si poteva intervenire, per poi elaborare un metodo che aiutasse gli studenti a migliorare i risultati delle prove INVALSI. La riflessione, però, non è stata rivolta solo alla costruzione di un nuovo metodo in base all’analisi dei risultati di partenza, ma è stata più ampia; infatti, prima di sviluppare la metodologia, si è intervenuti con l’analisi e l’individuazione delle competenze necessarie per il docente d’oggi.
I risultati INVALSI a confronto
Presentiamo innanzitutto il confronto tra i risultati delle prove di matematica degli ultimi quattro anni (2016, 2017, 2018, 2019) delle classi seconde degli istituti di scuola secondaria di secondo grado:
Figura 1
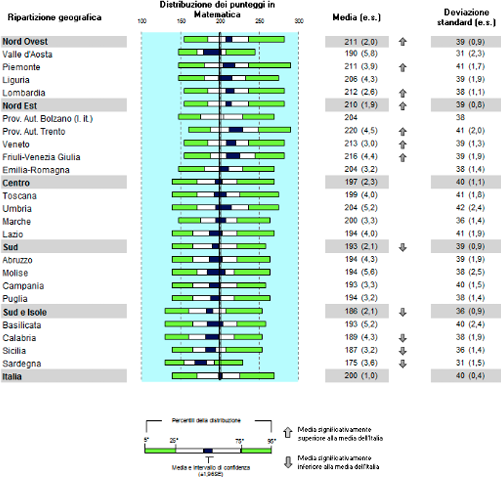
Risultati INVALSI 2016 in matematica delle Regioni (INVALSI, 2016, p. 46)
Figura 2
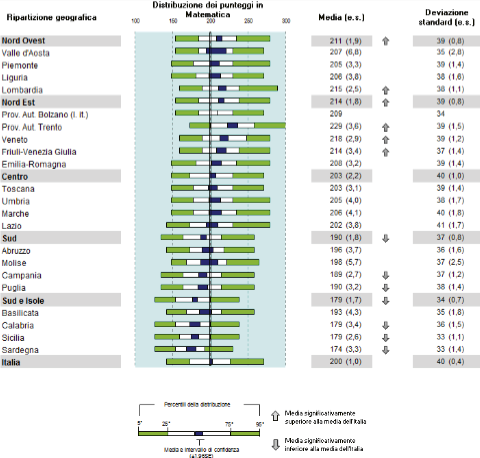
Risultati INVALSI 2017 in matematica delle Regioni (INVALSI, 2017, p. 47)
Figura 3
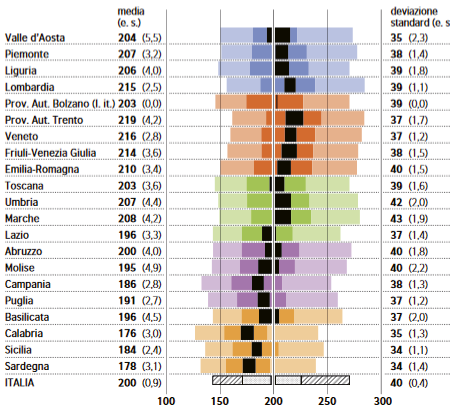
Risultati INVALSI 2018 in matematica delle Regioni (INVALSI, 2018, p. 53)
Figura 4
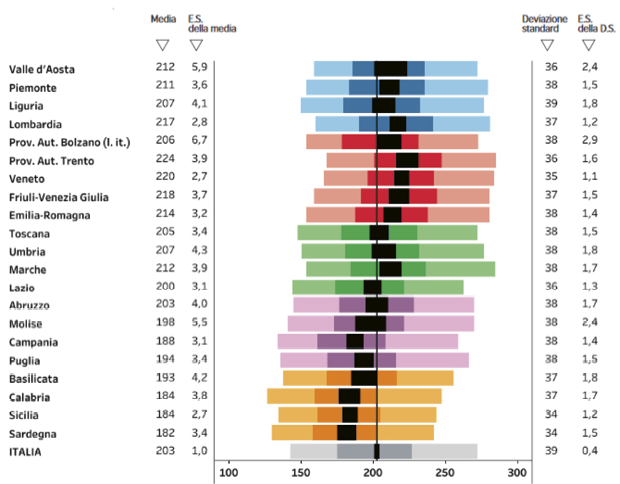
Risultati INVALSI 2019 in matematica delle Regioni (INVALSI, 2019, p. 70)
Le quattro regioni che più si discostano dalla media nazionale risultano essere la Campania, la Calabria, la Sicilia e la Sardegna. Si propone una sintesi degli andamenti, anno per anno, di queste regioni, maggiormente in difficoltà nei risultati di matematica:
Figura 5
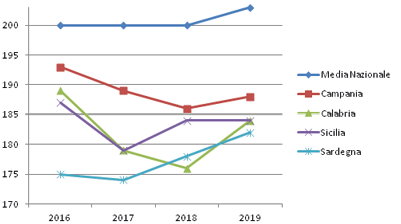
Confronto risultati INVALSI dal 2016 al 2019 nelle regioni più critiche. Fonte: produzione propria
La regione Campania, dopo anni di discesa, dimostra un miglioramento evidente, mentre per la Sardegna si evince un recupero costante. La Calabria migliora rispetto al picco negativo del 2018 e la Sicilia si mantiene invariata, nonostante il risultato negativo del 2017, ora superato. Per quanto riguarda la differenza dei risultati per tipologia di scuole secondarie, mostriamo solo i dati dell’ultimo anno (2019) che risultano essere di maggior interesse in particolare riferito alle regioni appena analizzate:
Figura 6
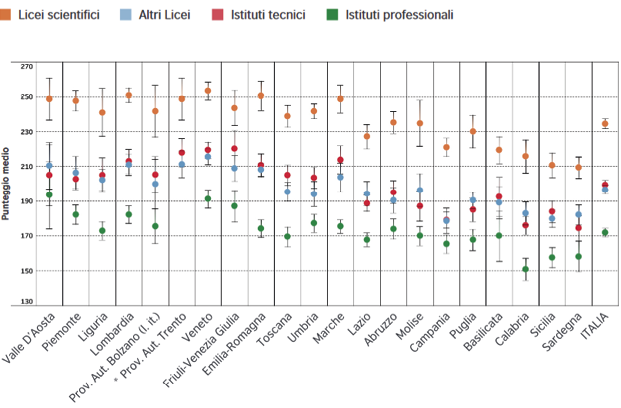
Risultati INVALSI 2019 in matematica delle Regioni per tipo di scuola (INVALSI, 2019, p. 72)
Dai dati in nostro possesso emerge che gli istituti professionali di Calabria, Sicilia e Sardegna hanno ottenuto i risultati maggiormente negativi, e si nota che in Campania risulta non positivo anche il riscontro ottenuto negli istituti professionali, mentre non si discosta di molto per altri licei e istituti tecnici, come invece avviene nelle altre regioni d’Italia.
Procedendo con l’analisi, ci si domanda quanti studenti abbiano raggiunto il cosiddetto «livello 3», considerato come traguardo corrispondente a un adeguato raggiungimento degli obiettivi posti nelle Indicazioni Nazionali/Linee Guida. In questo ulteriore passaggio, la percentuale di alunni che nel 2019 in seconda superiore raggiunge o supera il livello 3 per matematica è del 78% nel Nord Est e del 75% nel Nord Ovest, scende al 63% nel Centro (poco sopra la percentuale media a livello nazionale che è del 62%), e si abbassa ulteriormente, al 49% e al 43%, rispettivamente nel Sud e Isole. Più di metà degli alunni si colloca dunque in queste due aree al di sotto del livello 3.
La società delle competenze
Riconoscere le competenze chiave europee ha portato la società moderna a trasformarsi in una «società delle competenze»; viste nel loro complesso, le competenze chiave sembrano volte a soddisfare entrambi i paradigmi di cui scrive Baldacci (2014): il paradigma del capitale umano e il paradigma dello sviluppo umano, dove il primo mira a preparare produttori efficienti e il secondo mira all’espansione delle libertà sostanziali dei cittadini.
Quando si parla di competenze non si deve pensare solamente a quelle degli studenti bensì anche a quelle possedute dai docenti, ovvero tutte quelle necessarie affinché il docente possa svolgere al meglio la sua professione. Così la domanda che ci si è posti è stata: quali sono le competenze che deve possedere un docente di matematica oggi?
È bene sottolineare che un cambiamento della società, così rapido, ci sta portando all’esigenza di nuove strategie e allo sviluppo di differenti competenze per far sì che i nostri giovani studenti raggiungano gli obiettivi previsti. A rendere tale esigenza sempre più impellente non è stata solo la nascita delle otto competenze chiave di cittadinanza, ma anche il rapido sviluppo della tecnologia elettronica. I nostri ragazzi sono in molti casi nativi digitali e non possiamo ignorare che il mondo circostante è in gran parte diverso da quello che ha favorito la formazione dei loro docenti. Gli educatori devono educare i giovani all’uso critico e consapevole delle tecnologie — perché no, anche ricreativo! —, ma non annichilente.
Queste ragioni hanno condotto all’individuazione di alcune competenze fondamentali per i docenti di matematica oggi, ottenute a seguito di un’approfondita e costante ricerca bibliografico-sperimentale di tipo internazionale. Di seguito si riassumono tali competenze rielaborate nello schema che segue (Bocciolesi, Medina e Malvasi, 2019):
Figura 7
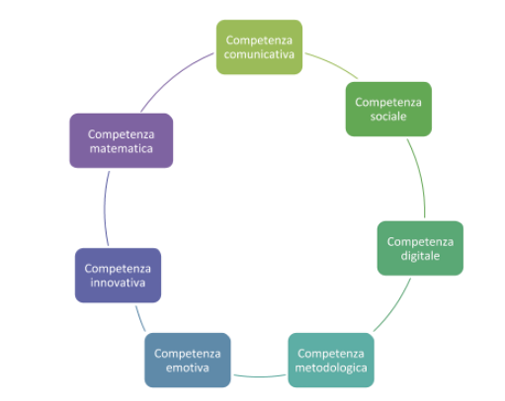
Competenze necessarie al docente di matematica. Fonte: produzione propria
Per la competenza comunicativa e la competenza sociale ci si è riferiti agli autori Dominguez e Garcìa (2012): si tratta di due competenze fondamentali per il docente, e nell’opera degli autori sono presenti anche suggerimenti su come migliorare nel loro dominio. Altra competenza oggi necessaria è quella digitale, in quanto ormai anche l’insegnamento e l’apprendimento richiedono l’uso di tecnologie elettroniche per il loro sviluppo, le quali danno un contributo rilevante in questi processi. Per questo motivo, gli Stati membri dell’Unione europea hanno riconosciuto la promozione della creatività e dell’innovazione, anche attraverso l’uso dei nuovi strumenti tecnologici e la formazione degli insegnanti, come una delle aree prioritarie per il primo ciclo del quadro strategico per l’Istruzione e Formazione 2020, detto ET 2020 (Unione europea, 2009). Per la competenza metodologica abbiamo richiamato Medina e il suo sistema Metodologico (2015). Nella competenza emotiva abbiamo tenuto conto dei contributi di Medina (2016) e Bocciolesi (2016). Per la competenza all’innovazione abbiamo preso in considerazione le tappe che, secondo Gairìn (2002), deve seguire un processo per definirsi innovativo: 1. definizione degli obiettivi; 2. pianificazione; 3. attuazione; 4. valutazione dei risultati.
E per questa ultima fase si sono presi in considerazione i metodi euristici di Medina (2015), che permettono di «misurare» l’efficacia dell’intervento stesso. Infine, per la competenza matematica, ci si è riferiti a Llinares (2016) e al suo mirar profesionalmente il pensiero matematico degli alunni. Tale competenza è specifica per l’area matematica o, per essere più precisi, si potrebbe ritenere specifica per tutta l’area scientifica (per materie come Fisica, Chimica, ecc.). Mirar profesionalmente letteralmente significa «guardare professionalmente», ovvero guardare con occhio esperto; tale competenza, secondo Llinares (2016), consiste nella capacità del docente di comprendere il livello di padronanza raggiunto dall’alunno in un dato argomento analizzando, con sguardo critico, le sue risposte. In altre parole, davanti a un quesito matematico, il docente non deve limitarsi a stabilire se la risposta dello studente sia giusta o sbagliata, ma deve avere la capacità di analizzare l’esito dell’attività, la quale gli fornisce un’interpretazione globale del livello di apprendimento raggiunto dall’alunno per l’argomento dato. Inoltre, un docente capace di mirar profesionalmente il pensiero matematico degli alunni, davanti a una risposta divergente rispetto all’aspettativa, permette di legittimare eventuali strategie utilizzate dall’alunno per risolvere un problema, in contrasto con il pensiero uniformato (Marcuse, 1968).
Dalle competenze al metodo
La prova INVALSI che si è somministrata al principio (INVALSI, 2016) è composta da 32 quesiti divisi in quattro Ambiti («Numeri», «Relazioni e Funzioni», «Dati e Previsioni», «Spazio e Figure») e tre Dimensioni («Conoscere», «Argomentare», «Risolvere problemi»). Analizzando i risultati di partenza ci si è trovati dinanzi a un’importante riflessione: «Conoscere» 17%, «Risolvere problemi» 39%, «Argomentare» 29%. Apparentemente sembravano dati contraddittori: come fanno i ragazzi a risolvere i problemi senza conoscere? D’altra parte, ci si rese conto che durante il primo anno erano stati proposti pochi compiti autentici agli alunni, lavorando scarsamente sull’aspetto «applicativo» dei numeri e della matematica in situazioni reali. Ed è questo profondo cambiamento ad averci orientato nell’analisi di partenza, vedendo la Dimensione «Risolvere problemi» come uno stimolo e non più come una Dimensione negativa e ardua. Così, rispetto a quanto fatto in passato, ci si è voluti concentrare su altre interpretazioni degli esiti, sui problemi autentici, sulla Dimensione «Risolvere problemi», per mostrare quel lato della matematica più affascinante. Mentre, fino ad allora, si era vista la Dimensione «Risolvere problemi» come una Dimensione che doveva fondare le sue basi sulla Dimensione «Conoscere», grazie ai risultati INVALSI e alle riflessioni che ne sono seguite, questa concezione è cambiata: si è scelto di vedere proprio quella Dimensione ritenuta maggiormente complessa come una prospettiva che può motivare i ragazzi ad apprendere l’uso e l’interpretazione degli strumenti matematici. In questo caso subentrano le emozioni e gli stimoli ad apprendere per riuscire a superare il limite visivo del codice numerico. Le sollecitazioni emozionali contribuiscono «ai successi nell’apprendimento, all’interiorizzazione di saperi e significati, al miglioramento dell’esperienza personale dell’adulto che apprende e che trasferisce e applica nel proprio ambito professionale i risultati di quanto appreso coinvolgendo le proprie risorse emotive» (Stefanini, 2013, p. 19).
Così «Risolvere problemi» passa dall’essere una Dimensione nemica ad essere una Dimensione amica. Se un problema autentico risveglia la curiosità nello studente, allora egli guarderà con nuovi occhi le espressioni, le rette, i sistemi lineari, le equazioni, ritenendo tutto maggiormente utile e sensato. Ecco perché si ritiene che dedicare maggior tempo alla Dimensione «Risolvere problemi» possa aiutare a cambiare la visione della matematica da disciplina per pochi a sapere per tutti, aumentando il rendimento della Dimensione «Conoscere». È necessario ripensare la disciplina e le considerazioni fino ad oggi prodotte, da talento matematico fino all’esclusività dell’essere portati per la matematica. Siamo, infatti, in completo accordo con ciò che dice Margiotta (2018) circa la concezione di talento da non intendersi come abilità innata a fare qualcosa meglio di altri. Inoltre, Margiotta ha sottolineato che, come si evince da recenti studi, anche qualora esista questa abilità innata, essa risulta irrilevante per spiegare le performance superiori; ciò che conta è un esercizio continuo e deliberato del proprio potenziale. Il talento si configura piuttosto come il risultato di un viaggio: rappresenta la forma con cui ci rappresentiamo agli altri e con cui gli altri ci percepiscono. Allora, con i «problemi giusti», la matematica può cambiare aspetto di fronte agli occhi curiosi e attenti degli studenti, ed è ciò che ci ricordano gli autori Fernández Cézar e Lahiguera Serrano (2015) con la rinominata Matemagia, vera e propria risorsa educativa. Il loro studio ha coinvolto 585 persone (555 alunni e 30 maestri) e con esso si è voluto misurare l’impatto sui bambini della matematica mediante l’uso di alcuni giochi di magia, prevedendo il ricorso a un matetrucco alla settimana. Nelle conclusioni si conferma che l’attenzione dei bambini è stata catturata e si è raggiunto un apprendimento significativo, non limitato all’uso numerico, ma coinvolgente per l’aspetto logico-riflessivo.
Per catturare l’attenzione degli alunni è necessario porre loro quesiti che siano vicini alla loro vita quotidiana. Ad esempio, chiedere: «Stefano ha un hard disk esterno che contiene: 
di film, 
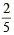di documenti e 
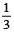di musica. Quanto spazio è occupato in percentuale nell’hard disk di Stefano?» è diverso che chiedere: «Sommare le seguenti frazioni , 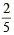e 
e poi trasformare il risultato in percentuale».
La riformulazione del pensiero matematico, adeguato alla necessità contestualizzata favorisce la reinterpretazione delle medesime regole logiche.
I pilastri del metodo
Dopo lo studio sulle competenze del docente e l’analisi dei risultati di partenza, si è prodotto un nuovo metodo, chiamato Metodo 360, che tenesse in conto le esigenze odierne del mondo della scuola.
Figura 8
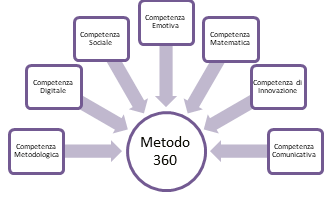
Metodo 360 e Competenze coinvolte. Fonte: produzione propria
Il Metodo 360 si basa principalmente su quattro pilastri (Bocciolesi, Medina e Malvasi, 2019):
- l’utilizzo sia di risorse tecnologiche elettroniche che di strumenti di uso comune o convenzionali, e l’integrazione tra collaborazione e autonomia (che lo rendono un metodo integrato);
- la necessità di porre una particolare attenzione e valorizzazione alle diversità degli studenti (che lo rende un metodo inclusivo);
- il focalizzare l’interesse sulla capacità di interpretare la matematica, di rileggere e comprendere il linguaggio matematico nella quotidianità (che lo rende un metodo interpretativo);
- l’innovazione e il relativo metodo euristico per verificare la validità del metodo (che lo rende un metodo innovativo).
Quindi il Metodo 360 può dirsi un metodo integrato, inclusivo, interpretativo e innovativo. Lo scopo della metodologia proposta è di raggiungere più studenti e docenti possibile, rispettando tempi e capacità di ognuno; questo metodo ha come scopo, anche se non primario, di cambiare la visione della matematica, vista spesso come una disciplina incomprensibile, ostica e accessibile solo a pochi; la matematica è una disciplina che educa al rigore e alla coerenza, che aiuta nello sviluppo delle capacità logiche e analitiche, ma al tempo stesso richiede intuito e creatività; ed è per tutti, non solo per alcuni. Nella costruzione del Metodo 360 si è cercato, tra gli altri obiettivi posti, di ridurre l’ostilità degli studenti nei confronti della disciplina, aumentando la fiducia nelle loro capacità.
Ambiti o Dimensioni
Dopo un’attenta analisi e una lunga riflessione sui dati di partenza, la situazione richiedeva una scelta: lavorare per Ambiti o per Dimensioni. Lavorare su entrambe sarebbe stato impossibile e approssimativo. Così si è deciso di lavorare sulle tre Dimensioni anziché sui quattro Ambiti per le seguenti ragioni.
- Il dato più preoccupante derivava dal 17% riferito alla Dimensione «Conoscere».
- A differenza dei quattro Ambiti, le tre Dimensioni sono trasversali; infatti, si è pensato che, se fossero migliorate le Dimensioni «Conoscere», «Risolvere problemi» e «Argomentare», sarebbero conseguentemente migliorati anche i risultati per i diversi Ambiti. Facciamo un esempio: se un alunno apprende ad argomentare, riuscirà a farlo sia nell’Ambito «Spazio e Figure» che nell’Ambito «Relazioni e Funzioni». Il contrario non è rilevabile: se uno studente migliora nell’Ambito «Numeri», non è detto che l’esito positivo si ripercuota sulla capacità di risolvere problemi o di argomentare.
Contesto dell’indagine e programmazione delle attività
All’inizio dell’anno scolastico (novembre 2016) è stata sottoposta la prova INVALSI del precedente anno scolastico ai ragazzi di una classe seconda di una scuola secondaria di secondo grado della regione Lazio (numero di studenti: 20), mentre nel maggio 2017 c’è stata la prova ufficiale. Ci si è serviti dei due momenti scolastici per avere a disposizione un pre e un post da confrontare. Il paragone, ovviamente, è avvenuto sia sul totale che sulle specifiche Dimensioni previste dall’INVALSI.
Tra una prova e l’altra sono state applicate una serie di strategie, tutte racchiuse in quello che si è denominato Metodo 360, per cercare di migliorare il rendimento degli alunni nelle prove INVALSI, soprattutto in quegli Ambiti e in quelle Dimensioni dove si erano riscontrate maggiori criticità (dai risultati di novembre).
Da novembre 2016 a maggio 2017, mettendo insieme tutte le teorie studiate ed esposte, gli spunti ricevuti e le risorse informatiche analizzate, si è finalmente deciso di cambiare approccio. Innanzitutto, si è ritenuto importante affrontare un numero maggiore di problemi autentici in classe. L’attività è stata impostata nel seguente modo: si è preparata una scheda su quesiti pratici, reperiti con diverse strumentazioni analogiche e digitali, dopodiché si è suddivisa la classe in piccoli gruppi eterogenei, per rendimento. L’attività è durata 40 minuti, i restanti 20 minuti si sono utilizzati per correggere i problemi insieme ai ragazzi, senza dare loro le soluzioni, bensì trovandole insieme. Dopo aver corretto gli esercizi in aula, il gruppo che aveva risposto a un maggior numero di quesiti riceveva uno stimolo, un più a ciascun membro del gruppo su di una griglia specifica, e al conseguimento di un certo numero di più i ragazzi ottenevano un incremento di mezzo voto nella successiva verifica. Questo tipo di incentivi/premi rientrano in quella che oggi chiamiamo gamification, termine che si riferisce non solo all’introduzione del gioco nella didattica, ma al trasformare la didattica basandola sulle meccanicità tipiche del gioco, come si fa in alcune applicazioni tipo ClassDojo (Gil Quintana, 2016). La cosa sorprendente è che alla fine la maggior parte della classe aveva accresciuto l’interesse verso la disciplina, sentendosi così, maggiormente abili. E avendo proposto dei problemi reali, che apparentemente non c’entravano nulla con la matematica, si è riscoperto un interesse, curiosità e spirito di gioco sopiti, rispetto a questa disciplina.
Un altro aspetto che non si è voluto trascurare è stato abituare gli studenti alle diverse tipologie di verifica (risposta multipla, vero o falso, risposta aperta).
Un’altra attività proposta in classe, che generalmente precede il giorno della verifica, è un gioco di squadra con quesiti misti che vertono sulle tre dimensioni Invalsi: «conoscere», «risolvere i problemi» e «argomentare». Si suddivide la classe in piccoli gruppi (da tre/quattro studenti) in linea con la peer collaboration, secondo la quale il gruppo può cooperare per trovare la risposta al quesito proposto. I vantaggi del collaborare sono innumerevoli; aiuta a non concepire più la diversità come un ostacolo, favorisce lo sviluppo di competenze sociali, ecc. Però, d’altro canto, favorendo la collaborazione tra gli alunni si ostacola lo sviluppo dell’autonomia degli stessi, con il fine di poter giungere al consolidamento delle proprie strategie di apprendimento, problem-posing e problem-solving. Le molteplici attività didattiche facilitano gli studenti nel dialogo, e per questo l’interazione tra di essi viene incentivata dal peer tutoring; facendo sì che tutti gli studenti siano chiamati a svolgere gli esercizi in autonomia, ricorrendo in caso di dubbi o errori al proprio compagno di banco. Con questa attività si crea un clima positivo e di autonomia, ma anche di aiuto reciproco. Ciò permette di creare una rete solida dove non si è soli ad aiutare chi non riesce a svolgere correttamente un esercizio, ma anche gli studenti più capaci, tutors, sono chiamati a fermarsi dallo svolgere il loro esercizio e a dedicarsi all’azione di tutoraggio nei confronti dei compagni che glielo chiedono. Il peer tutoring è una strategia inserita anche nel post-verifica, al bisogno: a volte, accade che una verifica vada male alla gran parte della classe, quindi è necessaria un’azione di recupero in itinere; per evitare che, nel ripetere lo stesso argomento, in alcuni prevalga la noia, si organizza un’azione di recupero mediante il peer tutoring. I gruppi sono stabiliti dal docente in base al profitto degli studenti e, ad ogni tutor, si assegnano poi uno/due studenti con maggiore difficoltà nella disciplina. Questa attività innalza l’autostima dello studente-tutor e permette di dare un sostegno personalizzato al ragazzo che ne ha bisogno, utilizzando un linguaggio ancora più adeguato.
Infine, si giunge al momento conclusivo di ogni attività: la verifica degli apprendimenti. Questa è una fase che è stata rivista totalmente dal nostro metodo: prima si credeva che per iniziare a porre e risolvere i problemi fosse necessaria una conoscenza di base dei numeri (naturali, interi relativi, razionali). Noi, invece, siamo convinti che per catturare l’interesse degli studenti sia necessario partire dai problemi. E per ognuno degli argomenti da approfondire, sono molti i problemi proposti, dai testi o dai supporti elettronici.
Come accennato in precedenza, per introdurre innovazione nelle scuole non è sufficiente proporre nuove strategie e idee. Affinché si possa parlare davvero di innovazione non può mancare la fase della valutazione della strategia applicata, che si può effettuare affiancando ad ogni metodo didattico un metodo euristico (Medina, 2015). La tabella 1 riassume i metodi euristici applicati a ogni attività svolta, dalla classica lezione frontale agli esercizi individuali, dalle esercitazioni di gruppo su problemi autentici alle attività in laboratorio, dai giochi a squadre con presentazione in Power Point alle verifiche scritte individuali.
Metodologia dell’indagine
Come metodologia di indagine si è scelto di svolgere un’indagine principalmente quantitativa per ottenere risultati oggettivi: uno studio sperimentale di campo, dove come variabile indipendente è stato fissato il Metodo 360 e come variabile dipendente da esso il rendimento degli alunni nelle prove INVALSI. Per misurare la variabile dipendente ci si è serviti di un pre-test e un post-test, e tra gli strumenti utilizzati c’è stata anche una scala di valutazione di tipo Likert di produzione propria e verificata mediante l’Alfa di Cronbach (Nunnally, 1978).
Nell’analisi dei risultati si è tenuto conto non solo della media raggiunta nelle varie Dimensioni e nei vari Ambiti, ma anche della deviazione standard in quanto è stato importante capire se una media elevata fosse prodotto della presenza di molte eccellenze, oppure se la distribuzione dei risultati risultasse abbastanza uniforme. Si è anche tenuto conto della deviazione standard delle medie in quanto, per alcuni casi, nonostante la percentuale risultante di un determinato Ambito o di una determinata Dimensione fosse scesa di qualche punto, la deviazione standard delle medie ci ha permesso di evidenziare la riduzione dei gap risultanti da novembre 2016 a maggio 2017.
Tabella 1
Elenco metodi euristici applicati a ogni attività
|
Attività proposta |
Metodo euristico |
|
Classica lezione frontale (con gesso e lavagna), con a seguire esempi |
Osservazione |
|
Esercizi individuali (scheda con le soluzioni); gli alunni possono chiedere aiuto ai loro compagni |
Osservazione |
|
Esercitazione di gruppo su problemi autentici (40 minuti + 20 minuti per la correzione) |
Scala di valutazione |
|
Attività in laboratorio: esercitazione individuale con la piattaforma «Aula 01 — Palestra Digitale» sulle diverse unità didattiche affrontate |
Scala di valutazione |
|
Gioco a squadre con presentazione in Power Point (spesso prima della verifica, attività di ripasso) |
Osservazione |
|
Verifica scritta individuale |
Risultati ogggettivi della prova |
Risultati
Ora vediamo i risultati oggettivi delle prove di novembre 2016 confrontati con quelli rilevati a maggio 2017. Iniziamo dal confronto dei risultati suddivisi per Ambiti (figura 9).
Figura 9
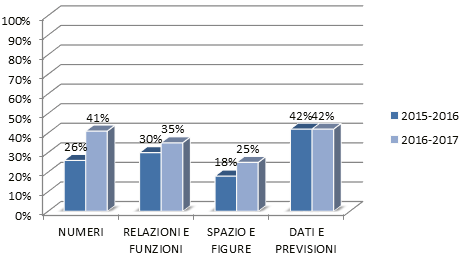
Risultati a confronto: gli Ambiti
Nell’Ambito «Dati e Previsioni» non si è riscontrato un cambiamento, mentre negli altri tre Ambiti il mutamento è risultato significativo.
Ora vediamo i risultati divisi per Dimensioni (figura 10).
Figura 10
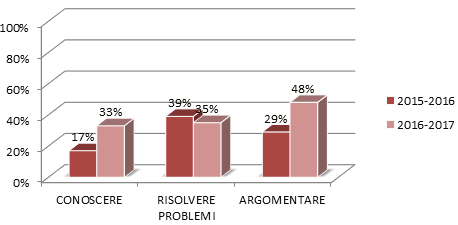
Risultati a confronto: le Dimensioni
In questo caso si vede un miglioramento su due Dimensioni di tre, ma la deviazione standard della Dimensione «Risolvere Problemi» è quella che è diminuita maggiormente rispetto alle altre, facendoci comprendere che il livello della classe si è avvicinato di più alla media.
Ora confrontiamo il totale delle risposte, sia per Ambiti che per Dimensioni (figure 11 e 12).
Figura 11
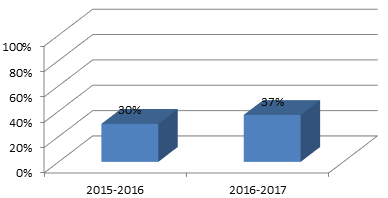
Totali a confronto: gli Ambiti
Figura 12
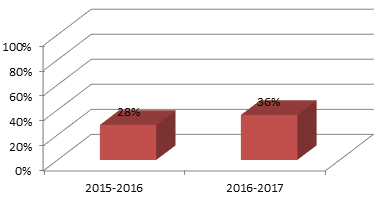
Totali a confronto: le Dimensioni
Il miglioramento non è molto più alto rispetto alla media nazionale, c’è ancora molto da ricercare, ma tali risultati evidenziano la positività del metodo proposto e degli approcci individuati. Inoltre, è necessario notare che con questi alunni si è lavorato con questo nuovo approccio solo dal secondo anno, quando, invece, si ritiene necessario applicarlo fin dal primo anno; in questo modo gli studenti possono sviluppare quelle competenze matematiche base, necessarie a ogni studente, futuro cittadino critico (Morin, 1985).
Conclusione
L’ipotesi di ricerca, centrata nell’applicazione in aula del Metodo 360, ha raggiunto l’obiettivo posto, l’ipotesi nulla è falsa. Inoltre, abbiamo potuto notare che mostrare il lato pratico della matematica, benché abbia prodotto una diminuzione di rendimento del 4% nella dimensione «Risolvere problemi», ha contribuito al rilevante miglioramento delle dimensioni «Conoscere» (+16%) e «Argomentare» (+19%), in quanto viene percepita come una materia più interessante, utile e pratica.
Partendo dalle competenze dei docenti e dall’analisi della situazione di partenza si è giunti a costruire il Metodo 360, che unisce le strategie che sostengono un nuovo approccio all’insegnamento della matematica. Le proposte educative, numerose, si sviluppano quindi con: la classica lezione frontale, l’esercitazione individuale in classe, l’esercitazione di gruppo su problemi autentici (40 minuti+20 minuti per la correzione), le attività in laboratorio, il gioco a squadre con presentazione interattiva, gli incentivi alla partecipazione in classe e al lavoro domestico; la verifica individuale e l’eventuale azione di recupero mediante peer tutoring.
Tale lavoro di ricerca e docenza richiede solide conoscenze pedagogiche per organizzare le numerose attività: preparare i materiali per l’esercitazione individuale, produrre e proporre i problemi autentici, organizzare i supporti tecnologici con i quesiti di ripasso per la verifica, preparare la verifica cercando le giuste domande per le differenti Dimensioni.
Concludiamo dicendo che il Metodo 360 ha permesso un miglioramento nei risultati INVALSI e di avvicinamento alla matematica, dimostrando con uno studio sperimentale di campo, la validità del sistema proposto. Quest’ultimo contiene tutte le connotazioni richieste oggi dal mondo della scuola: raggiungere tutti rispettando tempi e spazi, con occasioni di collaborazione e momenti di autonomia, servendosi sia delle risorse analogiche che digitali, offrendo incentivi per stimolare l’attenzione e la motivazione, in sintonia con i metodi euristici per misurare il livello degli obiettivi raggiunto a seguito delle attività svolte.
Bibliografia
Alessandrini G. (2017), Utopia contro disuguaglianza, giustizia contro potere, investimento in educazione contro la grande fuga, «FORMAZIONE & INSEGNAMENTO», vol. 15, n. 2, pp. 17-30.
Baldacci M. (2014), Per un’idea di scuola, Milano, FrancoAngeli.
Baldacci M. (2016), Logiche e aporie della meritocrazia. Appunti di lavoro, «Studium educationis», n. 3, pp. 21-27, https://ojs.pensamultimedia.it/index.php/studium/article/view/2419/2175 (consultato il 24 settembre 2020).
Bocciolesi E. (2016), Humanidad y Complejidad. Polifonìa de la Educaciòn, Madrid, Editorial Universitas S.A.
Bocciolesi E., Medina A. e Malvasi V. (2019), Comprendere e vivere la matematica nella docenza: Una proposta di ricerca tra strategie e competenze, Milano, Ledizioni.
Commissione Europea (2010), Comunicación de la Comisión al Parlamento Europeo, al Consejo, al Comité Económico y Social Europeo y al Comité de las Regiones – Una Agenda Digital para Europa, https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=COM:2010:0245:FIN:es:PDF (consultato il 24 settembre 2020).
D’Amore B. (2007), Epistemologia, didattica della matematica e pratiche d’insegnamento, «La matematica e la sua didattica», vol. 21, n. 3, pp. 347-369, http://www.dm.unibo.it/rsddm/it/articoli/damore/613%20Epistemologia%20did%20mat%20e%20pratiche%20di%20insegnamento.pdf (consultato il 24 settembre 2020).
Decreto Ministeriale 22 agosto 2007, n. 139, «Regolamento recante norme in materia di adempimento dell’obbligo di istruzione», https://www.cliclavoro.gov.it/Normative/D.M_22_agosto_2007_n.139.pdf (consultato il 24 settembre 2020).
Di Martino P. e Zan R. (2010), Me and maths: towards a definition of attitude grounded on students narratives, «Journal of Mathematics Teacher Education», vol. 13, n. 1, pp. 27-48. doi: 10.1007/s10857-009-9134-z
Domìnguez Garrido M.C. e Garcìa Gonzalez P. (2012), Tratamiento didáctico de las competencias bàsicas, Madrid, Editorial Universitas S.A.
Fernández Cézar R. e Lahiguera Serrano F. J. (2015), Matemagia y su influencia en la actitud hacia las matemáticas en la escuela rural, «Números. Revista de Didàctica de las Matematicas», vol. 89, pp. 33-53, http://www.sinewton.org/numeros/numeros/89/Articulos_02.pdf (consultato il 24 settembre 2020).
Gairìn J. (2002), Gestiòn de relaciones con el entorno. El cambio y la innovaciòn, in Master en Direcciòn y Gestiòn de Centros Educativos. UBA-Universidad de Deusto, modulo VII.
Gil Quintana J. (2016), ClassDojo, una APP monstruosa en Educación Infantil. Estudio de caso: CEIP Villalpando (Segovia), 5° Congreso de investigación educativa con impacto social (CIMIE), 29-30 giugno e 1° luglio, Siviglia.
Holubec E. J., Johnson D.W. e Johnson R.T. (2015), Apprendimento cooperativo in classe. Migliorare il clima emotivo e il rendimento, Trento, Erickson.
INVALSI (2016), Rilevazione Nazionale degli Apprendimenti 2015-2016. Rapporto Risultati, (consultato il 24 settembre 2020), http://www.INVALSI.it/INVALSI/doc_evidenza/2016/07_Rapporto_Prove_INVALSI_2016.pdf
INVALSI (2017), Rilevazione Nazionale degli Apprendimenti 2016-2017. Rapporto Risultati, http://www.INVALSI.it/INVALSI/doc_eventi/2017/Rapporto_Prove_INVALSI_2017.pdf (consultato il 24 settembre 2020).
INVALSI (2018), Rapporto Prove INVALSI 2018. Rapporto Nazionale, https://www.INVALSI.it/INVALSI/doc_evidenza/2018/Rapporto_prove_INVALSI_2018.pdf (consultato il 24 settembre 2020).
INVALSI (2019), Rapporto Prove INVALSI 2019. Rapporto Nazionale, https://INVALSI-areaprove.cineca.it/docs/2019/Rapporto_prove_INVALSI_2019.pdf (consultato il 24 settembre 2020).
Llinares S. (2016), Como dar sentido a las situaciones de enseñanza-aprendizaje de las Matematicas? Algunos aspectos de la competencia docente del profesor, «Cuadernos de Investigaciòn y Formaciòn en Educaciòn Matemàtica», vol. 11, n. 15, pp. 57-67, https://revistas.ucr.ac.cr/index.php/cifem/article/view/23944/24099 (consultato il 24 settembre 2020).
López-Barajas Zayas E., Gómez Mª J.A., Ortega Navas Mª C. e Ortega Sánchez I. (2009), El paradigma de la educación continua. Reto del siglo XXI, Madrid, Narcea-UNED.
Marcuse H. (1968), L’homme unidimensionnel, Parigi, Éditions de minuit.
Margiotta U. (2015), Teoria della formazione. Ricostruire la Pedagogia, Roma, Carocci.
Margiotta U. (2018), La formazione dei talenti come nuova frontiera, «FORMAZIONE & INSEGNAMENTO. Rivista internazionale di Scienze dell’educazione e della formazione», vol. 16, n. 2, pp. 9-14.
Marta-Lazo C. e Gabelas-Barroso J.A. (2016), Comunicación digital. Un modelo basado en el Factor R-elacional, Barcelona, Editorial UOC.
Medina A. (a cura di) (2015), Innovación de la educación y de la docencia, Madrid, Ramón Areces – UNED.
Medina M.C. (2016), La formación de Líderes en Inteligencia Emocional y Gestión del Talento, Madrid, Editorial Universitas S.A.
Morin E. (1985), La sfida della complessità, Milano, Feltrinelli.
Nunnally J.C. (1978), Psychonometric theory (2nd ed.), New York, McGraw-Hill.
Polya G. (1965), Cómo plantear y resolver problemas, México, Trillas.
Stefanini A. (2013), Le emozioni: Patrimonio della persona e risorsa per la formazione, Milano, Italia, FrancoAngeli.
UNESCO (2009), Investire nella diversità culturale e nel dialogo interculturale, http://unesdoc.unesco.org/images/0018/001847/184755ita.pdf (consultato il 24 settembre 2020).
Unione europea (2009), Istruzione e formazione. Collaborazione strategica a livello europeo (quadro ET2020), http://ec.europa.eu/education/policy/strategic-framework_it (consultato il 24 settembre 2020).
1 Dottoranda presso il Dipartimento di «Didáctica, Organización Escolar y Didácticas Especiales», UNED (Spagna), Universidad Nacional de Educación a Distancia.
2 Ricercatore presso il Dipartimento di «Didáctica, Organización Escolar y Didacticas Especiales», UNED, Universidad Nacional de Educación a Distancia.
3 Prof. Ordinario (già Direttore di Dipartimento) presso il Dipartimento di «Didáctica, Organización Escolar y Didácticas Especiales», UNED (Spagna), Universidad Nacional de Educación a Distancia.
4 PhD student at the Department of «Didáctica, Organización Escolar y Didácticas Especiales», UNED (Spagna), Universidad Nacional de Educación a Distancia.
5 Asst. Prof at the Department of «Didáctica, Organización Escolar y Didácticas Especiales», UNED (Spagna), Universidad Nacional de Educación a Distancia.
6 Full Professor (past Director of Department) at the at the Department of «Didáctica, Organización Escolar y Didácticas Especiales», UNED (Spagna), Universidad Nacional de Educación a Distancia.
Vol. 6, Issue 2, October 2020
