Vol. 21, n. 3, settembre 2022
PROSPETTIVE E MODELLI ITALIANI
Verso una didattica inclusiva della matematica per la scuola secondaria di primo grado
Heidrun Demo1, Marzia Garzetti1, George Santi2 e Giulia Tarini1
Sommario
Questo articolo presenta alcuni risultati preliminari del progetto di ricerca interdisciplinare (OPEN-MATH) che mira a contribuire a una didattica della matematica inclusiva, integrando il concetto di differenziazione, sviluppato all’interno della pedagogia e didattica speciale, e la teoria dell’oggettivazione, filone della didattica della matematica. Nello specifico, saranno qui presentate, utilizzando lo strumento della conjecture mapping, l’integrazione delle due prospettive teoriche e un modello progettuale coerente, l’Open Activity Theory Lesson Plan (OATLP). Attraverso la conjecture map si mostra come le metodologie didattiche riconducibili alla differenziazione didattica e alla teoria dell’oggettivazione diano forma a un modello progettuale che permette a livello teorico di definire la didattica inclusiva nell’ambito della classe di matematica, e di offrire strumenti di progettazione per unità di apprendimento sensibili alle caratteristiche di tutti e di ciascuno.
Parole chiave
Didattica inclusiva, Didattica della matematica, Didattica disciplinare, Teoria dell’oggettivazione, Differenziazione.
italian MODELS AND PERSPECTIVES
Towards an inclusive mathematics education for lower secondary education
Heidrun Demo3, Marzia Garzetti1, George Santi4 e Giulia Tarini1
Abstract
In the article some preliminary results of the interdisciplinary research project (OPEN-MATH) are presented. The project aims to contribute to inclusive mathematics education by integrating the concept of differentiation, developed within special pedagogy and didactics, and the theory of objectification, a strand of mathematics education. Specifically, the integration of the two theoretical perspectives and a coherent lesson plan, the Open Activity Theory Lesson Plan (OATLP), will be presented here using conjecture mapping. By means of the conjecture map, it will be shown how teaching and learning methods that can be traced back to differentiation and the theory of objectivation contribute both to define the inclusive mathematics classroom on a theoretical level and to offer design tools for learning units that are sensitive to everyone’s learning characteristics.
Keywords
Inclusive education, Inclusive classroom, Mathematics education, Theory of objectification, Differentiated classroom.
Introduzione
Questo articolo presenta la prima fase di ricerca del progetto OPEN-MATH, finanziato dalla Libera Università di Bolzano. Il progetto mira a contrastare le disuguaglianze attraverso lo sviluppo di teorie, metodologie e pratiche per una didattica disciplinare inclusiva, e in particolare per una didattica della matematica inclusiva per la scuola secondaria di primo grado.
Nello specifico, la prima fase del progetto OPEN-MATH ha visto la costruzione dell’impostazione teorica sottesa al modello didattico implementato, l’Open Activity Theory Lesson Plan (OATLP). Tale lavoro ha permesso di costruire un dialogo interdisciplinare tra didattica della matematica e didattica inclusiva attraverso la riflessione sulla progettazione di un intervento educativo. Nell’articolo si presenteranno le prospettive teoriche dei ricercatori coinvolti e si metterà in evidenza il ruolo di tali prospettive nella costruzione del modello OATLP. Il conjecture mapping (Sandoval, 2014) è la tecnica, propria dell’Educational Design Research (McKenney and Reeves, 2019), a cui si è fatto ricorso per chiarire e visualizzare le varie ipotesi fatte nelle diverse fasi della ricerca: tale tecnica verrà presentata in relazione al percorso fino ad ora svolto poiché chiarisce in modo esplicito come il modello OATLP sia legato a una specifica visione della classe e dell’apprendimento in matematica, e quali siano i risultati attesi dalla sua implementazione in termini di inclusione.
L’articolo non vuole fornire dati sull’impatto dell’implementazione del modello, ancora in fase di sperimentazione ed elaborazione, ma mostrare come si possa impostare una progettazione che leghi l’attenzione agli aspetti disciplinari, in questo caso legati all’apprendimento della matematica, e l’attenzione all’inclusione in senso più generale. Per fare ciò, si introdurranno inizialmente le motivazioni alla base del progetto. In seguito si definiranno le prospettive teoriche e i riferimenti su cui OPEN-MATH si forma: la definizione di inclusione, gli approcci alla didattica inclusiva e alla didattica della matematica scelti e la tecnica del conjecture mapping. Si lascerà poi spazio alla presentazione del modello OPEN-MATH propriamente detto, a partire proprio dalla struttura della conjecture map del progetto, che permette di mettere in luce il legame tra teoria, progettazione e processi di apprendimento.
Motivazioni al progetto
La scuola secondaria di primo grado di fronte alle disuguaglianze
Nel 1962 la nuova scuola media «unica» è nata proprio con l’intento di contribuire alla crescita della scolarità, nell’ottica dell’uguaglianza delle opportunità formative. Da allora, le carriere scolastiche si sono allungate, ma le pari opportunità sono ancora lontane dall’essere realizzate (Fondazione Giovanni Agnelli, 2014). I dati mostrano che proprio la scuola secondaria di primo grado è un momento particolarmente critico nelle carriere delle ragazze e dei ragazzi italiani.
Rispetto ai risultati di apprendimento che alunne e alunni conseguono nella scuola secondaria, le disuguaglianze esistono e sono forti: fra regioni, fra scuole all’interno delle stesse regioni e fra alunne e alunni con storie diverse (dell’Anna, 2021; INVALSI, 2020; OECD, 2018). Lo status socio-culturale di provenienza continua a impattare fortemente i risultati di apprendimento sia agli inizi che sul finire del percorso formativo, così come il genere. Pur con tutte le cautele che la lettura dei dati INVALSI richiede, in generale, nell’ultimo anno di scuola secondaria di primo grado una percentuale compresa fra il 30% e il 40% delle alunne e degli alunni non raggiunge un livello considerato in linea con le indicazioni nazionali in italiano e matematica (INVALSI, 2020). Va inoltre evidenziato che non vi sono dati sul valore aggiunto prodotto dalla scuola nei percorsi di apprendimento di alunne e alunni con disabilità, DSA o più in generale BES (dell’Anna, 2021).
In questo contesto la matematica, considerata una delle discipline fondamentali del percorso scolastico (MIUR, 2012), assume particolare rilievo. La crescente preoccupazione per le difficoltà legate a questa disciplina e le disparità osservate tra gli studenti nel processo di apprendimento (Atweh et al., 2011) hanno portato a considerazioni e riflessioni di carattere etico e politico con oggetto la matematica stessa, e quindi la sua didattica in termini generali (Ernest, 2019; Radford, 2021). Imparare la matematica può diventare un’esperienza negativa per molti studenti, con un impatto significativo sul percorso scolastico individuale. Inoltre, una visione della matematica che non tenga in considerazione le implicazioni etiche delle sue applicazioni può diventare dannosa per l’individuo e la società (Ernest, 2019). Sviluppare la didattica della matematica in prospettiva inclusiva è, in questo contesto, una strada per superare, tra gli altri, i rischi legati a percorsi formativi che tengano conto solo degli aspetti più specificatamente disciplinari, aprendosi alle implicazioni sociali ed etiche dell’insegnamento della matematica oltre che a combattere le disuguaglianze e promuovere equità di esperienze formative.
Le didattiche disciplinari inclusive
Sebbene esistano riflessioni trasversali sulla didattica inclusiva e sulle metodologie didattiche utili a realizzarla applicabili nel contesto della progettazione disciplinare nella scuola secondaria (Tomlinson, 2014; CAST, 2011), emerge la necessità di mettere a disposizione della scuola secondaria di primo e secondo grado un sapere capace di coniugare in modo coerente le riflessioni legate alle discipline con quelle legate all’inclusione. Tale sapere, caratterizzato da forte interdisciplinarità, è in larga misura ancora da sviluppare. Questo è evidente in una recente analisi della letteratura che traccia un quadro delle review di studi empirici condotte nell’ambito dell’inclusive education fino al 2016 e mette in luce come il tema della didattica disciplinare inclusiva sia largamente sottoesplorato (Van Mieghem et al., 2020). Anche in Italia un recente mapping degli articoli di ricerca nell’ambito della pedagogia speciale e della pedagogia dell’inclusione pubblicati fra il 2009 e il 2019 mette in rilievo come non sia stata pubblicata alcuna ricerca che affronti in termini complessivi un modello per una didattica disciplinare inclusiva nel territorio nazionale (Bellacicco e dell’Anna, 2019).
In questo filone di ricerca, la matematica può essere considerata un cantiere particolarmente interessante: negli ultimi anni, infatti, l’attenzione alle differenze individuali di alunne e alunni si sta affermando come una dimensione fondamentale dei processi di insegnamento e apprendimento anche in questo ambito (un esempio è dato dal lavoro di Santi e Baccaglini-Frank, 2015). Diversi studi hanno inoltre messo in luce come i più diffusi test per i disturbi di apprendimento non permettano di comprendere in modo differenziato e puntuale le difficoltà individuali di alunne e alunni e di distinguere chiaramente quali difficoltà derivino da un determinato tipo di didattica e quali da un effettivo disturbo dell’apprendimento (Baccaglini-Frank e Bartolini Bussi, 2016). In questo senso, l’apprendimento della matematica può diventare un’opportunità per sviluppare specifiche competenze che favoriscono la creatività, l’autodeterminazione, l’interazione sociale per ciascuno studente secondo le sue caratteristiche, nell’ottica di riflettere e interagire con una realtà socioculturale, in cui essa riveste un ruolo di rilievo. Inoltre, da una recente review della letteratura sul modo in cui è stata affrontata l’inclusione nell’ambito della didattica della matematica (Roos, 2019), appare evidente come le ricerche sull’inclusione in matematica mostrino ancora evidenti limiti. Tendono infatti a posizionarsi su poli distinti e difficilmente interagenti: da un lato, discussioni di carattere teorico sulla definizione di inclusione in matematica; dall’altro, design di interventi educativi dichiaratamente inclusivi in cui il concetto di inclusione non viene però problematizzato e definito nell’ambito di applicazione.
Il progetto OPEN-MATH si inserisce in questo contesto, e il lavoro qui presentato mostra come si possano mettere in relazione, tramite la tecnica del conjecture mapping propria dell’Educational Design Research, i due poli descritti da Roos (2019) con l’obiettivo di valorizzare nella prassi didattica la diversità degli studenti, superando l’idea di approcci specifici per determinate categorie.
Prospettive teoriche di riferimento
Inclusione scolastica, politiche e didattica
Nella riflessione pedagogica, si è storicamente assistito a un passaggio nel tempo da definizioni più strette di inclusione, focalizzate sulla presenza di alunne e alunni con disabilità o bisogni educativi speciali nei contesti educativi ordinari e sulla qualità dei loro percorsi, a definizioni più ampie che vertono su una scuola democratica e di qualità per tutte le alunne e tutti gli alunni (Göransson & Nilholm, 2014). In questa seconda accezione l’inclusione è intesa come un processo che mira a identificare e superare eventuali barriere che ostacolano alcuni alunne e alunni nell’accesso all’educazione e nel raggiungimento di risultati ottimali, sia in fatto di apprendimento che di socializzazione (Ainscow, 2016).
Anche sul piano delle politiche educative per l’inclusione, il trend è quello di uno spostamento da un modo più stretto di intendere l’inclusione, a uno più ampio, come rilevato dalle ricerche dell’Agenzia Europea sui Bisogni Educativi Speciali (Meijer e Watkins, 2019). Allo stesso tempo, però, appare evidente una certa contraddittorietà e confusione di approcci stretti e ampi che deriva dal fatto che nella maggior parte dei Paesi le politiche educative inclusive in senso ampio sono il frutto di un’evoluzione storica di quelle strette che raramente hanno portato a un ripensamento globale e coerente (D’Alessio, Donnelly e Watkins, 2010; Opertti, Zachary e Zhang, 2014). Nel contesto italiano incoerenze di questo tipo sono ben visibili e richiami al principio generale di una scuola inclusiva intesa in senso ampio si affiancano a misure di supporto specifiche per singole categorie di alunni identificati come alunni con disabilità, disturbi specifici dell’apprendimento o bisogni educativi speciali. Questo diventa evidente, per esempio, nel recente decreto 66/2017 che apre con un articolo 1 dedicato a una scuola inclusiva che mira a valorizzare le differenze di tutte le alunne e tutti gli alunni e a sviluppare un contesto di apprendimento che garantisca percorsi di apprendimento e socializzazione di qualità per tutti, ma, allo stesso tempo, è l’incipit di un documento legislativo che si occupa di inclusione in senso «stretto», volto alla messa a punto di misure specifiche per alunni con disabilità. In questo senso, la visione «ampia», pur essendo accennata, convive con una visione più «stretta».
In questo contesto, anche la didattica inclusiva è attraversata da un’ambivalenza. Da un lato, infatti, essa si propone come «progettazione, nella realizzazione e nella valutazione di azioni educative che attivano i processi di apprendimento e partecipazione di tutti gli alunni e di tutte le alunne» (Demo, 2018, p. 109). Dall’altro, essa richiama alla necessità di tenere conto delle specificità dei diversi funzionamenti individuali, come nel caso di alcuni alunni con disabilità oppure di alunni plurilingui con storie di migrazione, promuovendo l’autodeterminazione di ciascuno e ciascuna. Emerge qui un dilemma costitutivo della didattica inclusiva. Per promuovere la partecipazione e l’apprendimento di tutte e tutti, la didattica deve al contempo: 1) essere sensibile alle differenze, lasciare spazio a diversi processi e percorsi e alla loro autoregolazione senza privilegiarne alcuni; 2) riconoscere le similarità di tutte e tutti nell’essere parte di una comunità condivisa e partecipata. Nel fare questo, se si supera l’uso di misure specifiche per alcuni, si rischia un poco equo appiattimento delle differenze (Shakespeare, 2017) e, invece, potenziandole, si rischia l’attivazione di forme di stigmatizzazione ed etichettamento (Algraigray e Boyle, 2017). Diversi autori in diversi contesti culturali hanno riflettuto su questo aspetto (Ianes, 2006; Norwich, 2008), spesso nominato come «dilemma della differenza»: per gestire tale dilemma e promuovere la partecipazione e l’autodeterminazione di ciascuno studente attraverso la didattica, il progetto OPEN-MATH fa riferimento alla differenziazione didattica proposta da Carol Ann Tomlinson (2014).
Il piano metodologico della didattica inclusiva
In questo senso, il piano metodologico della didattica inclusiva richiede una progettazione che alterni momenti e setting volti a creare uno spazio in cui ciascun alunno e ciascuna alunna possa seguire un proprio individuale e unico percorso di apprendimento, compiendo scelte consapevoli, e altri, invece, che offrono un’opportunità per un agire collaborativo e in cui ciascuno possa contribuire a suo modo a un progetto comune. Questa visione si ritrova anche nella proposta della differenziazione didattica sviluppata da Carol Ann Tomlinson che pone alla base di una gestione inclusiva della classe, da un lato, il principio per cui ciascun alunno debba essere riconosciuto nella sua unica e irripetibile unicità, ma dall’altro anche quello per cui queste differenze devono potersi ricomporre in un progetto di classe a cui ciascuno a suo modo possa partecipare (Tomlinson, 2014).
Un ampio ventaglio di metodologie sostiene la realizzazione di questa visione. L’attenzione alla singolarità di ciascun’alunna e ciascun alunno, per esempio, può essere ben veicolata da quelle metodologie didattiche che fanno riferimento alla didattica aperta, come la didattica a stazioni o le agende settimanali (Demo, 2016). La didattica aperta è un approccio basato sulla libera scelta di alunne e alunni: il percorso di apprendimento non è progettato dalle/dagli insegnanti e realizzato da ragazze e ragazzi, ma prevede un ruolo attivo degli alunni nel determinare il percorso da attivare e seguire. La prospettiva centrata sull’alunno focalizza l’attenzione sull’apprendimento invece che sull’insegnamento e incoraggia lo sviluppo di ambienti di classe in cui i processi di apprendimento sono decentralizzati e plurali: diversi studenti lavorano su diversi compiti e ognuno di loro sta attraversando il proprio prezioso processo di apprendimento. Questo permette di realizzare una differenziazione per tutti gli alunni. In secondo luogo, la centralità della libertà di scelta da parte di alunne e alunni introduce la possibilità di una «differenziazione autodeterminata»: in un paesaggio di apprendimento che offre molteplici opportunità, gli insegnanti non hanno più bisogno di progettare per ciascuno studente la consegna più adatta, ma sostengono la scelta autonoma e competente da parte di ragazze e ragazzi.
Metodologie, invece, come l’apprendimento per progetti (Lotti, 2018) o l’apprendimento cooperativo (Cohen, 1999) possono contribuire a organizzare occasioni per la partecipazione di ciascuno a un percorso comune. In ciascuna di queste proposte è evidente come, pur basandosi su attività da svolgere in grande o piccolo gruppo, il contributo individuale possa essere valorizzato proprio nell’ottica delle differenze individuali. Centrali in questo senso sono le riflessioni di autrici e autori che hanno studiato come facilitare e sostenere la partecipazione di ciascuno nel gruppo. Cohen (1999), per esempio, mette in evidenza l’importanza di individuare consegne «aperte», consegne cioè che permettono a gruppi diversi di arrivare a risultati diversi, egualmente corretti, ma sensibili alle differenze individuali dei membri del gruppo. Oppure ancora segnala l’importanza di creare situazioni in cui ciascun alunno e alunna possa sentire gli altri membri del gruppo come una risorsa e il prodotto del lavoro di gruppo come un risultato a cui nessuno da solo sarebbe arrivato. Perché questo accada, alcune strutture, come per esempio l’attribuzione esplicita di ruoli può essere particolarmente utile.
Due indicatori di inclusione: autodeterminazione e partecipazione
Prima di procedere, è utile definire meglio due termini che torneranno nella descrizione del progetto: autodeterminazione e di partecipazione. Sono termini che caratterizzano l’approccio inclusivo a più livelli. Quando si parla di partecipazione (Ianes et al., 2021) a una comunità di apprendimento si intende la possibilità di essere presenti alle attività che vengono svolte, di agire su tale ambiente, di essere riconosciuti e di apportare un contributo; quando si parla di autodeterminazione si intende il rispetto dei percorsi individuali e delle scelte operate da ciascuno e ciascuna, della possibilità stessa di compiere scelte che si adattino alla propria soggettività (Cottini, 2016).
Gli ambienti di apprendimento inclusivi promuovono la partecipazione e l’autodeterminazione, quindi, per valutare il grado di inclusione, è necessario rendere partecipazione e autodeterminazione operativamente rilevabili nel contesto classe, e nell’agire degli studenti. La partecipazione è considerata, a partire da un adattamento del lavoro di Ianes, Cramerotti e Fogarolo (2021, p. 408), come partecipazione sociale, definita in relazione alla comunità di appartenenza dell’individuo. Nel contesto considerato, quello della classe di matematica, la partecipazione coincide con l’interazione tra alunne e alunni e insegnante a diversi livelli: si ha partecipazione se un soggetto risponde a interazioni iniziate da altri, se lui stesso avvia interazioni, se si indirizza il lavoro del gruppo o si porta l’attenzione dei pari o dell’insegnante su temi che si ritengono rilevanti. La mancanza di partecipazione per lo studente si ha quando questi è assente, è marginalizzato, o è presente ma non interagisce con i compagni.
Un individuo autodeterminato è invece tale se «agisce come agente causale primario della propria vita» (Cottini, 2016, p. 17). L’agire come agente causale si attua su quattro dimensioni secondo l’autore: l’autonomia nello svolgere compiti o prendersi cura di sé, ma anche nello scegliere; l’autoregolazione nella pianificazione e nel problem solving; l’empowerment psicologico nel considerarsi efficaci autori del proprio percorso e del proprio successo; e autorealizzazione intesa come consapevolezza dei propri punti di forza e limiti.
Nella classe queste quattro componenti si osservano in diversi momenti del lavoro, sia individuale sia di gruppo, nei momenti di scelta, nelle attività di problem solving, nella riflessione sul proprio operato o durante la valutazione tra pari, e vengono incentivate esplicitamente tramite l’approccio della differenziazione didattica, che lavora proprio sul fornire allo studente la possibilità di determinare il proprio percorso formativo insieme all’insegnante.
Didattica della matematica nella teoria dell’oggettivazione
La teoria dell’oggettivazione è la teoria dell’apprendimento della matematica di riferimento nel progetto OPEN-MATH: fa parte delle teorie socioculturali contemporanee che vedono l’individuo come consostanziale alla cultura, o alle culture, in cui vive. Oltre a costituirsi come lente per l’indagine dei fenomeni associati all’apprendimento della matematica, la teoria dell’oggettivazione ha un forte carattere trasformativo: punta infatti a «creare soggetti riflessivi ed etici che si posizionano criticamente nelle pratiche matematiche storicamente e socialmente costituite, considerando nuove possibilità di azione e di pensiero» (Radford, 2021, p. 24 tradotto). Per questo motivo, e per l’attenzione sia al soggetto che apprende sia alla cultura in cui l’apprendimento avviene, la teoria è stata scelta nel progetto. È importante rimarcare che, con i termini «soggetti riflessivi ed etici», Radford (2021) intende sia gli studenti sia gli insegnanti, immaginandoli impegnati in un percorso di apprendimento che assume la forma di un lavoro congiunto (joint labour). Il conoscere in questo senso chiama in causa l’etica, poiché coinvolge il rapporto con l’altro nella costruzione di una comunità e di una cultura in cui e per cui si è reciprocamente responsabili. Il sapere matematico non è un bene che transita dall’uno all’altro, o che si costruisce individualmente, ma si materializza nel rapporto dialettico tra cultura e joint labor, attraverso l’uso di segni e artefatti (linguaggio, gesti, simboli, oggetti, ecc.). Tali segni e artefatti sono la manifestazione della cultura, sono portatori di significati prodotti dall’attività intellettuale delle generazioni precedenti (Radford, 2021) e permettono di osservare l’apprendimento in atto.
In questa teoria si considerano le due facce dell’apprendimento, che è da un lato processo di oggettivazione e dall’altro di soggettivazione. Il processo di oggettivazione è «il processo attivo, embodied, discorsivo, simbolico e materiale attraverso cui gli studenti incontrano sistemi culturalmente e storicamente costituiti di pensiero, riflessione e azione» (Radford 2021, p. 35, tradotto). Mentre il processo di soggettivazione è il processo tramite cui l’individuo, nell’incontro con l’oggetto di conoscenza, si trasforma e si posiziona criticamente e creativamente nella pratica matematica. Nel processo di soggettivazione, l’individuo diventa una presenza nel mondo che realizza il suo progetto di vita (Radford, 2020). Proprio in questo elemento si manifesta la stretta relazione con l’idea di una didattica inclusiva intesa come dialogica di differenza/specialità e comunanza/normalità. La soggettivazione è infatti intesa come un processo differente per ciascun’alunna e alunno a seconda dei propri talenti, bisogni e interessi. Ciò avviene parallelamente al processo di oggettivazione, percorso in cui tutta la comunità di apprendimento, insieme, si confronta con i segni e gli artefatti del sapere matematico, rilevanti per la cultura del luogo e del tempo che insieme viene abitato.
In questo senso, la matematica, come «sapere ideale e generale» (Radford, 2021), è un sistema dinamico di modelli fissi e archetipi di pratiche, riconosciuto e codificato storicamente e culturalmente. Il passaggio dal sapere ideale alla sua concretizzazione avviene nel joint labour: un processo multimodale (simbolico, percettivo, senso-motorio, materiale) mediato da segni e artefatti. La multimodalità tipica della matematica, che coinvolge linguaggio, movimenti, gesti, e artefatti, permette, in ottica inclusiva, di considerare quelle che sono le diverse forme specifiche di ciascun allievo di apprendere la matematica come processo di oggettivazione, adattabili alla pluralità degli studenti della classe.
Sul piano metodologico, la Teoria dell’Oggettivazione propone un proprio design metodologico chiamato Activity Theory Lesson Plan (Radford, 2015). Coerentemente coi riferimenti teorici appena descritti, tale design si basa sull’idea che l’apprendimento avvenga nell’interazione fra studenti, insegnanti e artefatti e si costituisce di un ciclo di attività che alterna momenti di lavoro in piccolo e in grande gruppo che prendono avvio dalla presentazione di un problema o attività matematica. Tali attività devono essere definite a partire da un elemento del sapere matematico, inteso come archetipo di attività che coinvolge determinati artefatti (si parla ad esempio di saper risolvere algebricamente problemi di un determinato tipo, saper misurare l’estensione di una figura facendo uso di strumenti adeguati, ecc.) e che rappresenta l’obiettivo dell’attività. Il problem solving permette l’oggettivazione, poiché sostiene un’attività significativa in cui lo studente incontra il sapere matematico in gioco usando gli artefatti a sua disposizione nella direzione di risolvere il problema proposto, ed è questo aspetto che viene osservato all’interno della classe, insieme al joint labour, al lavoro congiunto che si realizza e permette la partecipazione di ciascuno al processo di apprendimento.
La tecnica del conjecture mapping nell’Educational Design Research: costruire relazione tra prospettive teoriche e progettazione didattica
Nel tentativo di coniugare le prospettive descritte e di progettare pratiche d’aula inclusive si è scelto l’approccio metodologico della Educational Design Research (EDR) (McKenney e Reeves, 2019) poiché ha lo scopo esplicito, da un lato, di far progredire la comprensione teorica dei processi di apprendimento e di insegnamento e, dall’altro, di progettare interventi didattici per affrontare i problemi o i bisogni che sorgono nei contesti educativi. Parafrasando McKenney e Reeves (2019), l’EDR cerca di creare soluzioni efficaci a problemi educativi, e di identificare nuove conoscenze in relazione a tali problemi, spesso sotto forma di principi di progettazione di attività di insegnamento. L’EDR mira a individuare dei principi di progettazione che siano implementabili e permettano di affrontare il problema scelto, nel caso presentato l’inclusione in matematica, e al contempo di rendere espliciti i legami di tali principi con le teorie considerate e con i risultati attesi, in modo da lavorare sull’integrazione degli stessi in una nuova e più ampia prospettiva. In questo senso il progetto OPEN-MATH lavora su ciò che Roos (2019) identifica essere un collegamento mancante tra pratiche d’aula inclusive e la problematizzazione del termine inclusione in relazione alla didattica della matematica.
Nel progetto si è utilizzata la tecnica del conjecture mapping (Sandoval, 2014) propria dell’EDR per rendere esplicita la struttura argomentativa della ricerca: i legami tra assunzioni teoriche e ipotesi relative alla progettazione di classe. La conjecture map permette di definire quelli che sono le caratteristiche alla base di un intervento didattico, i loro legami con i processi osservati in aula e i risultati attesi.
La struttura della conjecture map si articola in quattro colonne, descritte in figura 1.
Figura 1
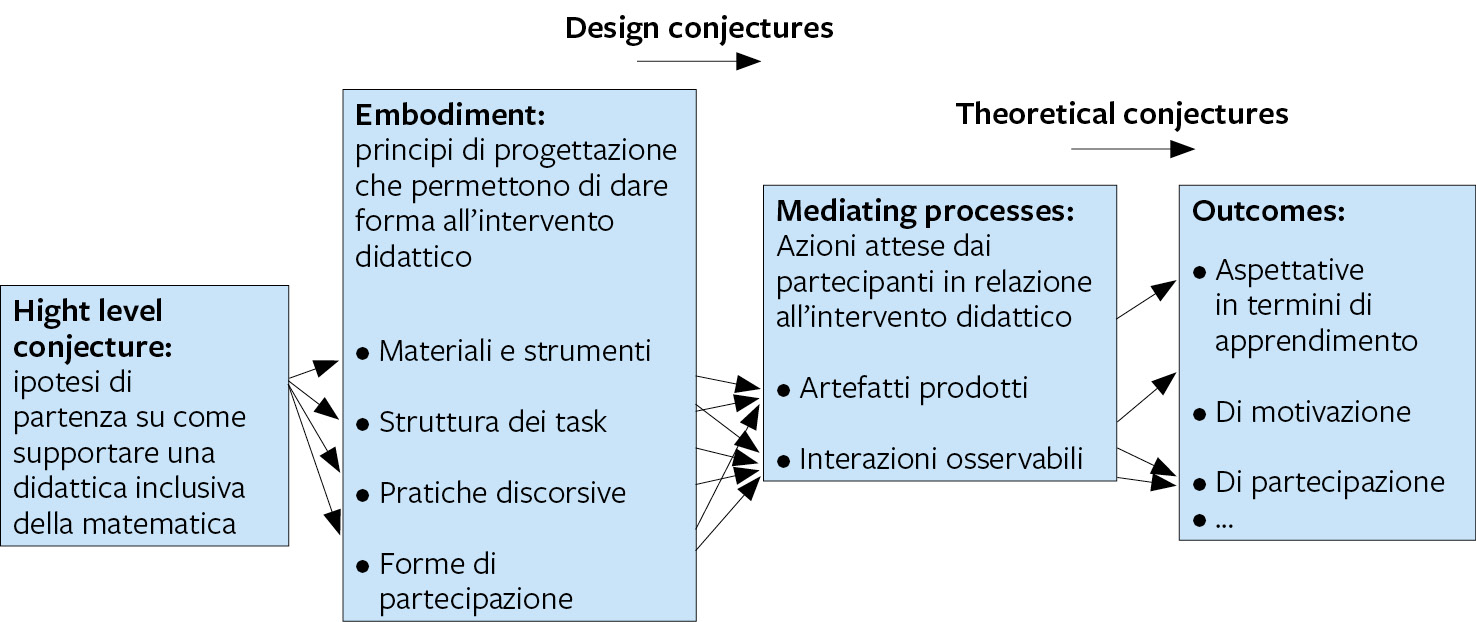
Presentazione degli elementi costitutivi di una conjecture map (Sandoval, 2014).
In questo articolo si presenterà la conjecture map associata a una possibile progettazione didattica inclusiva, descritta nella sezione successiva, che cerca di unire i risultati provenienti dall’ambito della didattica inclusiva e della didattica della matematica descritti nelle sezioni precedenti.
La proposta di OPEN-MATH per una didattica inclusiva della matematica
La domanda di ricerca affrontata nel progetto OPEN-MATH si può riassumere come segue.
Quali caratteristiche ha una progettazione didattica che promuova l’inclusione nella classe di matematica fondata sull’integrazione della teoria dell’oggettivazione e del paradigma inclusivo, in particolare dalla differenziazione didattica? In che modo possiamo aspettarci che la progettazione impatti sulle pratiche d’aula e sui risultati di alunne e alunni?
Si presenta in questa sezione la conjecture map del progetto, che permette di mostrare come le assunzioni di partenza proprie dei paradigmi adottati, e le metodologie didattiche a cui si fa riferimento, si coniughino in una proposta progettuale, e come questo determini le aspettative rispetto alla sua implementazione. In figura 2 si presenta la conjecture map del progetto, e in seguito se ne commentano le diverse colonne.
Figura 2
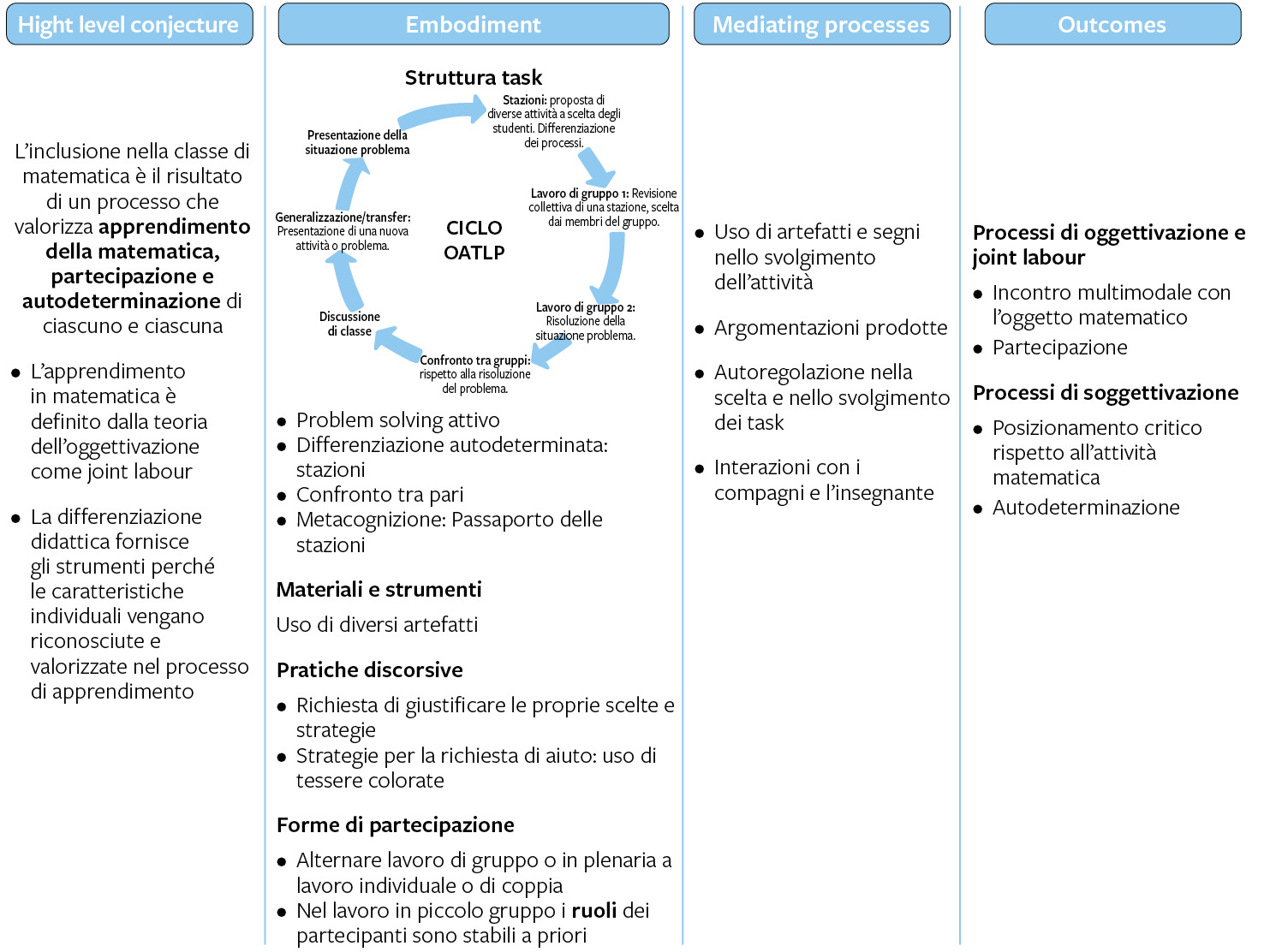
La conjecture map del progetto OPEN-MATH.
Si può osservare come l’high level conjecture nella prima colonna faccia diretto riferimento all’idea di inclusione nella classe di matematica frutto dell’integrazione degli approcci sopra descritti: la teoria dell’oggettivazione e la differenziazione didattica. Proprio a partire da questi approcci si è dato forma a un lesson plan, un modello di progettazione, volto a conciliare l’importanza dell’interazione sociale e del senso di appartenenza, all’attenzione alle differenze individuali nel percorso di apprendimento.
Nel seguito si descrive nel dettaglio la seconda colonna della conjecture map, che mostra il ciclo di attività progettato insieme alle sue principali caratteristiche.
Embodiment: come l’intervento educativo attua i principi educativi di partenza
Il ciclo OATLP, presentato per maggiore chiarezza anche in figura 3, è strutturato a partire dall’Activity Theory Lesson Plan (ATLP) proposto nella teoria dell’oggettivazione: a partire da una situazione problema costruita introno a un particolare obiettivo di apprendimento, si alternano attività di gruppo ad attività da svolgersi con l’intera classe che accompagnano il gruppo verso il raggiungimento dell’obiettivo. Nell’Open-ATLP (OATLP) sono stati aggiunti alcuni momenti di apertura didattiche che permettono la differenziazione dei processi di apprendimento.
Le Stazioni (Demo, 2016; Tomlinson, 2014) sono una delle possibili strategie legate all’implementazione di una didattica aperta e sono un modo per mettere in pratica la differenziazione sviluppando ambienti di classe in cui i processi di apprendimento sono decentralizzati e plurali: nello specifico, allo studente vengono proposte diverse attività, associate a uno stesso obiettivo didattico. Nella proposta sviluppata per l’Embodiment, alunne e alunni possono scegliere quali attività svolgere e se svolgerle in autonomia o con un compagno. In questa fase, le modalità di aiuto reciproco e richiesta di chiarimenti sono codificate, per permettere all’insegnante di gestire la classe e ai ragazzi di diventare risorsa l’uno per l’altro. A questo scopo, ciascuno studente ha a disposizione cartellini di diverso colore che permettono visivamente di capire se sta lavorando bene in autonomia, se ha bisogno dell’aiuto di un pari, o se ha bisogno di un confronto con un docente. In linea con i principi progettuali propri della differenziazione didattica esposti in Sousa e Tomlinson (2011), si sviluppano le diverse stazioni avendo come principio guida il fornire una varietà di modalità di accesso alla conoscenza sulla base delle caratteristiche specifiche della classe, che vengono indagate nel corso dell’anno, anche tramite attività specifiche (per alcuni esempi vedere Tomlinson, 2014). Inoltre, il fatto che gli studenti possano scegliere in autonomia, introduce una differenziazione autodeterminata (Demo, 2016) in cui lo studente diventa consapevole del proprio percorso di apprendimento a livello globale.
Figura 3
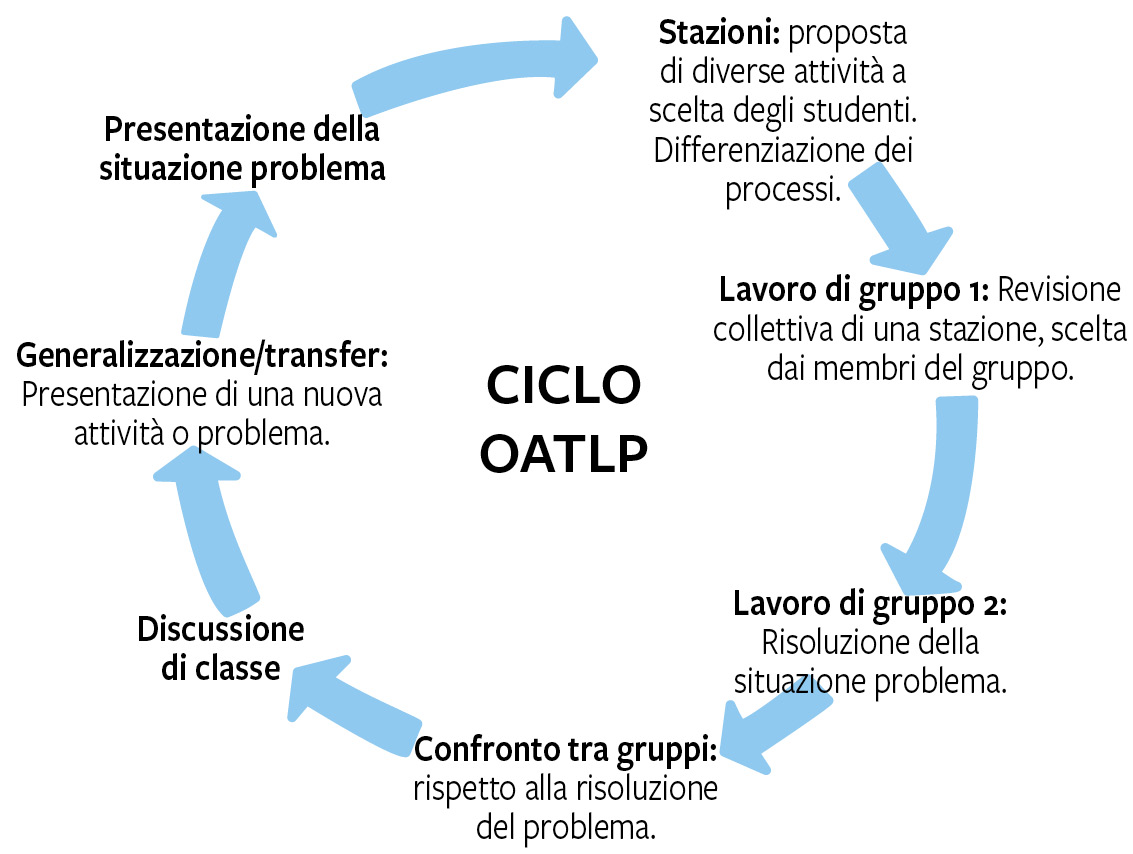
Modello didattico dell’Open Activity Theory Lesson Plan.
La molteplicità di artefatti delle stazioni, associati a uno stesso oggetto matematico, permette l’oggettivazione del sapere incentivando la multimodalità, quindi l’intervento di diversi canali sensorali (visivi-verbali, visivi-non verbali, uditivi e cinestesici). La stessa scelta degli artefatti è un momento fondamentale della progettazione proprio perché nella teoria dell’oggettivazione gli artefatti stessi sono visti come portatori di un sapere storico-culturale, in questo caso matematico (Radford, 2021).
Al termine del lavoro a stazioni lo studente compila un «passaporto» in cui annota le stazioni completate, le difficoltà incontrate e ciò che gli ha permesso di imparare nel modo più efficace o piacevole: il passaporto è un momento in cui lo studente riflette sul suo apprendimento e il suo percorso, ma permette anche all’insegnante di tenere traccia dei diversi percorsi, oltre che di organizzare i momenti successivi dell’attività. Nel lavoro di gruppo 1, la revisione collettiva di una stazione all’interno del gruppo permette un primo momento di confronto tra pari, in cui si rimettono in gioco strategie e scelte fatte individualmente, si argomentano decisioni prese o possibili soluzioni.
In generale, lungo tutto il ciclo vi è una forte attenzione alla definizione di consegne aperte (Tomlinson, 2014; Cohen, 1999), che permettano a ognuno di posizionarsi secondo le proprie abilità e caratteristiche nell’attività, sviluppando pratiche collaborative di lavoro con i compagni, e consapevolezza del proprio percorso di apprendimento. Nel lavoro di gruppo, i problemi sono scelti proprio in relazione ai due criteri, quello di apertura della consegna e quello della significatività matematica (Radford, 2021). Inoltre, per facilitare la collaborazione in questa fase vengono attribuiti dei ruoli agli studenti (Cohen, 1999).
L’attività di confronto tra gruppi è caratteristica della metodologia della teoria dell’oggettivazione (Radford, 2015): aiuta gli studenti a motivare le proprie scelte e a considerare alternative, sia sul piano della comunicazione dei contenuti sia sul piano dell’efficacia o della correttezza delle strategie. La discussione di classe coincide con il momento di condivisione e istituzionalizzazione, a cui segue l’attività di generalizzazione, in cui vengono proposti agli studenti nuovi problemi o nuove attività relative all’obiettivo didattico fissato. Il momento di generalizzazione può essere impostato a stazioni in base alla situazione degli studenti al termine della discussione, o tramite una consegna aperta che permetta di richiamare le diverse attività svolte durante l’intero ciclo.
Aspettative sull’implementazione: mediating processes e outcomes
Ciascuna delle caratteristiche del ciclo di attività è associata a pratiche d’aula, specifiche azioni attese dagli studenti nel momento dell’implementazione. Tali azioni sono, in forma schematica, categorizzate nella terza colonna, relativa ai mediating processes. Si può osservare come ciascun principio di progettazione sia legato ad alcune azioni, o interazioni, in classe. Alcune, come l’uso dei segni e degli artefatti, sono legate alla teoria dell’oggettivazione in modo specifico. La teoria dell’oggettivazione fornisce infatti strumenti per interpretare il significato di tali usi a partire dall’analisi degli artefatti e segni utilizzati e per individuare i diversi livelli di concettualizzazione matematica a cui lo studente può lavorare, più legati alla manipolazione di artefatti concreti o alla generalizzazione di simboli. Altre caratteristiche del modello OATLP sono invece legate a pratiche d’aula che vedono il singolo studente nella possibilità di autoregolarsi nel processo di apprendimento e di essere autonomo in alcune sue fasi (Cottini, 2016).
Ciascuna di queste pratiche d’aula è associata nella quarta colonna a un outcome atteso: gli outcomes sono strutturati rispetto a oggettivazione e soggettivazione. La teoria dell’oggettivazione è infatti una teoria dell’apprendimento che tiene conto sia dell’incontro del soggetto con la cultura, nei processi di oggettivazione, sia della trasformazione a cui il soggetto va incontro mentre apprende, nei processi di soggettivazione. Questa doppia attenzione, al sapere matematico e all’individuo, che apprendendo diviene soggetto culturale, è fondamentale per parlare di inclusione in matematica come apprendimento (matematico in questo caso) e piena partecipazione a un contesto culturale. Per questo motivo, i processi di oggettivazione e soggettivazione strutturano gli outcomes attesi, ma al contempo vengono integrati dai due indicatori specifici di inclusione: partecipazione (Ianes et al., 2021) e autodeterminazione (Cottini, 2016). L’attenzione a questi indicatori permette di esplicitare quanto i fenomeni osservati riescano a tenere conto delle peculiarità di ognuno nel processo di apprendimento inteso nei due sensi, come incontro col sapere, e come formarsi del soggetto.
Si vede quindi che l’oggettivazione è considerata tale quando si hanno sia un uso cosciente di segni e artefatti coinvolti nell’attività, sia una partecipazione attiva del singolo nell’interazione (Ianes et al., 2021). Analogamente, la soggettivazione si attua sia nel posizionamento critico dello studente, osservabile tramite l’argomentazione in classe nelle sue diverse forme, sia nell’autodeterminazione (Cottini, 2016), associata invece ad autonomia e autoregolazione osservate.
Il risultato atteso in termini di progettazione è l’inclusione di ciascuno e ciascuna, inclusione che è intesa come apprendimento, partecipazione e autodeterminazione sin nelle assunzioni iniziali del progetto: la conjecture map permette però di strutturare in processi osservabili tale risultato, coniugando autenticamente le due prospettive teoriche di partenza in caratteristiche di design, processi attesi e outcomes ad essi associati.
Una pratica educativa inclusiva raggiunge il suo scopo quando unisce l’oggettivazione del sapere in termini di joint labour, con la scelta e la realizzazione del progetto di vita di ciascuno e ciascuna. È così che l’inclusione del soggetto si manifesta anche nel suo posizionamento critico rispetto a una pratica storicamente affermatasi, che avviene a partire da quelle che sono le sue peculiarità, bisogni, e i suoi contributi alla disciplina stessa.
Conclusioni e prospettive
Il progetto OPEN MATH si configura come un progetto-pilota che mira a identificare alcune piste di ricerca significative per la didattica inclusiva nella scuola secondaria a partire da risultati provenienti dalla didattica inclusiva, in particolare dalla differenziazione didattica, e dalla didattica della matematica, in particolare dalla teoria dell’oggettivazione.
Uno dei risultati più rilevanti della prima fase del progetto riguarda la possibilità di integrare e connettere teorie e concetti della didattica della matematica con quelli della didattica inclusiva. Nel processo descritto da questo articolo, per esempio, si è visto come il concetto di differenziazione possa diventare un elemento radicato nella didattica della matematica, nel momento in cui l’apprendimento, definito come processo di oggettivazione e soggettivazione, viene associato a partecipazione e autodeterminazione. Questa integrazione si fa veicolo di un passaggio culturale importante, quello per cui la didattica disciplinare, in questo caso della matematica, si fa di per sé inclusiva, trasformandosi essa stessa: è così che l’attenzione alle differenze individuali diviene parte costitutiva di un’idea formalizzata di didattica disciplinare. Altrimenti, il rischio che essa sia concepita in termini di «aggiunta o appendice» è alto, spesso dando avvio a pratiche che rischiano di introdurre elementi di stigmatizzazione e strisciante marginalizzazione (Prediger e Burò, ٢٠٢١; Galanti, Giaconi e Zappaterra, 2021). Alla base di questo vi è un percorso interdisciplinare che ha, in questa fase embrionale, necessità di un investimento di ricerca, e che richiede una riflessione profonda sul modo in cui i principi della didattica inclusiva possono essere integrati nelle didattiche disciplinari.
La matematica, come evidenziato all’inizio di questo articolo, è un ambito di studio importante in questo senso: la ricerca in didattica della matematica ha da diversi anni mostrato l’importanza di superare un’idea di intervento didattico volto a supportare i soli studenti con bisogni educativi speciali, in un’idea stretta di inclusione, andando verso l’attenzione a caratteristiche e differenze individuali (es. Santi e Baccaglini-Frank, 2015; Baccaglini-Frank e Bartolini Bussi, 2016). OPEN-MATH si fa promotore di questa prospettiva, proponendo un modello didattico che ha alla sua base un’idea di inclusione ampia, quella della differenziazione didattica, e che costruisce su di essa i suoi principi di progettazione integrandoli con l’attenzione all’apprendimento della matematica.
Il progetto di ricerca si colloca inoltre in un filone metodologico di ricerca che mira a superare la frattura fra teoria e pratica: si è visto ad esempio come parlare di inclusione nell’ambito della didattica della matematica spesso significhi posizionarsi solo su uno di questi due poli (Roos, 2019). Inoltre, si è osservato come quello della didattica disciplinare inclusiva sia un tema che necessita attenzione e studio (Van Mieghem et al., 2020): parlando di scuola secondaria di primo grado italiana, non parlare di didattica disciplinare significa restare al di fuori della strutturazione del percorso di studenti e insegnanti, e quindi di nuovo creare una frattura fra ricerca e pratica. Nel progetto OPEN-MATH si vogliono allora coniugare la pratica didattica e lo sviluppo di interventi educativi alla generazione di un sapere che vada oltre la specifica proposta didattica. Nel caso specifico di questa ricerca la tecnica del conjecture mapping (Sandoval, 2014) ha permesso di mettere in luce la possibilità di lavorare coerentemente su questi due livelli in ambito di progettazione e di messa a punto di strumenti di ricerca interdisciplinari utili a valutare il grado di partecipazione, di autodeterminazione e di apprendimento dei singoli alunni e alunne nell’attuazione di interventi educativi specifici, grazie all’associazione tra embodiment, mediating processes e outcomes attesi.
Si sono, tramite questa prima fase del lavoro di ricerca, poste le basi per l’implementazione di un modello di didattica inclusiva della matematica per la scuola secondaria di primo grado. In prospettiva più allargata, il progetto può proporsi come esempio per lo sviluppo delle didattiche disciplinari in prospettiva inclusiva in diversi ambiti, tramite l’adozione di un percorso analogo di strutturazione delle ipotesi di ricerca e di esplicitazione dei legami tra le teorie adottate.
Bibliografia
Ainscow M. (2016), Diversity and equity: A global education challenge, «New Zealand Journal of Educational Studies», vol. 51, n. 2, pp. 143-155.
Algraigray H. e Boyle C. (2017), The SEN label and its effect on special education, «The Educational and Child Psychologist», vol. 34, n. 4, pp. 70-79.
Atweh B., Graven M., Secada W. e Valero P. (a cura di) (2011), Mapping equity and quality in mathematics education, New York, Springer.
Baccaglini-Frank A. e Bartolini Bussi M. (2016), Buone pratiche didattiche per prevenire falsi positivi nelle diagnosi di discalculia: Il progetto PerContare, «Form@re», vol. 15, n. 3, pp. 170-184.
Bellacicco R. e Dell’Anna, S. (2019), Trend e gap nella ricerca sull’inclusione scolastica in Italia: una Mapping, «Le Società per la società: ricerca, scenari, emergenze», Atti del Convegno Internazionale SIRD, pp. 45-53.
CAST (2011), Universal Design for Learning (UDL) Guidelines version 2.0., Wakefield, CAST [Traduzione in italiano versione 2.0 (2015) a cura di Giovanni Savia e Paolina Mulè].
Cohen E.G. (1999), Organizzare i gruppi cooperativi. Ruoli, funzioni, attività, Trento, Erickson.
Cottini L. (2016), L’autodeterminazione nelle persone con disabilità: percorsi educativi per svilupparla, Trento, Erickson
D’Alessio S., Donnelly V. e Watkins A. (2010), Inclusive education across Europe: the move in thinking form integration for inclusive, «Revista de Psicología y Educación», vol. 1, n. 5, pp. 109-126.
dell’Anna S. (2021), Modelli di valutazione di un sistema scolastico inclusivo, Milano, FrancoAngeli.
Demo H. (2016), Didattica aperta e inclusione, Trento, Erickson.
Demo H. (2018), Didattica Inclusiva. In L. d’Alonzo (a cura di), Dizionario di pedagogia speciale per l’inclusione, Brescia, Morcelliana.
Ernest P. (2019), Privilege, power and performativity: the ethics of mathematics in society and education, «Philosophy of Mathematics Education Journal», n. 35.
Fondazione Giovanni Agnelli (2014), La valutazione della scuola, Roma-Bari, Laterza.
Galanti M.A., Giaconi C. e Zappaterra T. (2021), Didattiche e progettazioni: storie e tracce evolutive verso l’inclusione, «Italian Journal of Special Education for Inclusione», vol. 9, n. 1, pp. 7-14.
Göransson K. e Nilholm C. (2014), Conceptual Diversities and Empirical Shortcomings – A Critical Analysis of Research on Inclusive Education, «European Journal of Special Needs Education», vol. 29, n. 3, pp. 265-280.
Ianes D. (2006), Speciale Normalità, Trento, Erickson.
Ianes D., Cramerotti S. e Fogarolo F. (2021), Il nuovo PEI in prospettiva bio-psico-sociale ed ecologica, Trento, Erickson.
INVALSI (2020), Rapporto prove Invalsi 2019, Roma, INVALSI.
Lotti A. (2018), Problem-Based Learning: Apprendere per problemi a scuola: guida al PBL per l’insegnante, Milano, FrancoAngeli.
McKenney S. e Reeves T. C. (2019), Conducting educational design research, London, Routledge.
Meijer C.J.W. e Watkins A. (2019), Financing special needs and inclusive education. From Salamanca to the present, «International Journal of Inclusive Education», vol. 23, n. 7-8, pp. 705-721
MIUR (2012), Indicazioni nazionali per il curricolo della scuola dell’infanzia e del primo ciclo d’istruzione, Roma.
Norwich B. (2008), Dilemmas of difference, inclusion and disability: International perspectives and future directions, London, Routledge.
OECD (2018), Equity in Education: Breaking Down Barriers to Social Mobility, Paris, OECD Publishing.
Opertti R., Zachary W. e Zhang Y. (2014), Inclusive education: From targeting groups and schools to achieving quality education as the core of EFA. In Florian L. (a cura di), The SAGE Handbook of Special Education, London-New York, Sage, pp. 149-169.
Prediger S. e Buró R. (2021), Fifty ways to work with students’ diverse abilities? A video study on inclusive teaching practices in secondary mathematics classrooms, «International Journal of Inclusive Education», pp. 1-20.
Radford L. (2015), Methodological Aspects of the Theory of Objectification, «Perspectivas da Educação Matemática», vol. 8, n. 18, pp. 547-567.
Radford, L. (2020), Play and the production of subjectivities in preschool. In M. Carlsen, I. Erfjord e P.S. Hundeland (a cura di), Mathematics education in the early years. Results from the POEM4 conference 2018, Cham, Springer, pp. 43-60.
Radford L. (2021), The Theory of Objectification: A Vygotskian Perspective on Knowing and Becoming in Mathematics Teaching and Learning, Leiden-Boston, Brill.
Roos H. (2019), Inclusion in mathematics education: an ideology, a way of teaching, or both?, «Educational Studies in Mathematics», vol. ١٠٠, pp. ٢٥-٤١.
Sandoval W. (2014), Conjecture mapping: An approach to systematic educational design research, «Journal of the learning sciences», vol. 23, n. 1, pp. 18-36.
Santi G. e Baccaglini-Frank A. (2015), Forms of generalization in students experiencing mathematical learning difficulties, «PNA», vol. 9, n. 3, pp. 217-243.
Shakespeare T. (2017), Disabilità e Società, Trento, Erickson.
Sousa D.A. e Tomlinson C.A. (2011), Differentiation and the brain: How neuroscience supports the learner-friendly classroom, Bloomington, IN, Solution Tree Press.
Tomlinson C.A. (2014), The differentiated classroom: Responding to the needs of all learners, Alexandria, VA, Ascd.
Van Mieghem A., Verschueren K., Petry K. e Struyf E. (2020), An Analysis of Research on Inclusive Education: A Systematic Search and Meta Review, «International Journal of Inclusive Education», vol. 24, n. 6, pp. 675-689.
Vol. 21, Issue 3, September 2022


